题目内容
 如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
考点:全等三角形的判定与性质
专题:
分析:(1)根据DE⊥AC,BF⊥AC可以证明DE∥BF;再求证Rt△ABF≌Rt△CDE可得BF=DE,即可解题;
(2)根据(1)中结论可证△DEM≌△BFM,即可解题.
(2)根据(1)中结论可证△DEM≌△BFM,即可解题.
解答:解:(1)DE=BF,且DE∥BF,
证明:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°.
∴DE∥BF,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE;
(2)在△DEM和△BFM中,
,
∴△DEM≌△BFM(AAS),
∴MB=MD.
证明:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°.
∴DE∥BF,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
|
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE;
(2)在△DEM和△BFM中,
|
∴△DEM≌△BFM(AAS),
∴MB=MD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证Rt△ABF≌Rt△CDE是解题的关键.

练习册系列答案
相关题目
下列物体的性状类似于球的是( )
| A、茶杯 | B、羽毛球 |
| C、西瓜 | D、文具盒 |
校运会上,八年级共有17位同学参加200米预赛,已知他们所跑的时间互不相同,现有8个决赛名额.王同学知道自己的比赛成绩后,要判断自己能否进决赛,在下列17名同学成绩的统计量中只需知道一个量,它是( )
| A、众数 | B、方差 |
| C、中位数 | D、平均数 |
已知
=-
,x:y的值是( )
| x-y |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中,则关于x的不等式0<k2x<k1x+b的解集为
如图,直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中,则关于x的不等式0<k2x<k1x+b的解集为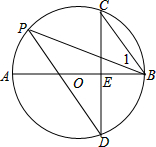 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,