题目内容
13.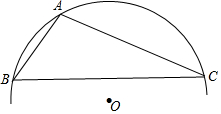 己知,△ABC;
己知,△ABC;(1)求作:△ABC 的外接圆⊙O(尺规作图,保留作图痕迹);
(2)若∠B=60°,AC=8,求⊙O的半径.
分析 (1)利用三角形外接圆的作法得出圆心的位置进而得出即可;
(2)连接OA、OC,由圆周角定理得出∠AOC=120°,进一步由垂径定理得∠AOD=60°,AD=4,最后根据OA=$\frac{AD}{sin∠AOD}$可得答案.
解答 解:(1)如图所示:⊙O即为所求;
(2)连接OA、OC,
∵∠B=60°,
∴∠AOC=120°,
又∵OD⊥AC,且AD=CD,AC=8,
∴∠AOD=60°,AD=4,
则OA=$\frac{AD}{sin∠AOD}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{8\sqrt{3}}{3}$,
即⊙O的半径为$\frac{8\sqrt{3}}{3}$.
点评 本题主要考查三角形的外接圆的作法及圆周角定理、垂径定理的运用,熟练掌握三角形外接圆上的点到三角形的三顶点的距离相等是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
3.已知图中的两个三角形全等,则∠1等于( )


| A. | 52° | B. | 60° | C. | 68° | D. | 70° |
4.用16cm长的铁丝围成一个等腰三角形,则腰长可以是( )
| A. | 3cm | B. | 4cm | C. | 7cm | D. | 9cm |
1. 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(l,m),则不等式mx>kx+b的解集是( )
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(l,m),则不等式mx>kx+b的解集是( )
 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(l,m),则不等式mx>kx+b的解集是( )
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(l,m),则不等式mx>kx+b的解集是( )| A. | x>l | B. | x<2 | C. | x<l | D. | x>2 |
8.下列计算中,正确的是( )
| A. | (a2)4=a6 | B. | a8÷a4=a2 | C. | (ab2)3=ab6 | D. | a2•a3=a5 |
18.下列命题中,真命题有( )
①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形对的一个外角大于任何一个内角;④如果a2=b2,那么a=b.
①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形对的一个外角大于任何一个内角;④如果a2=b2,那么a=b.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列各组数中互为相反数的是( )
| A. | 2与|-2| | B. | -2与$\sqrt{(-2)^{2}}$ | C. | -2与-$\frac{1}{2}$ | D. | -2与$\root{3}{-8}$ |