题目内容
14. 为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
分析 (1)植2株的有16人,所占百分比为32%,则可求出其总人数,根据计算结果结合图表找出众数;结合(1)的数据将条形统计图补充完整;
(2)先根据“植树3株”的人数为50-9-16-7-4=14(人),且所占总人数比例:14÷50=28%,即可得到“植树3株”对应扇形的圆心角的度数;
(3)根据题意,求得其平均数为2.62,超过平均数的为25人,根据概率公式进行计算即可.
解答 解:(1)该班的总人数:16÷32%=50(人);
因为植3株的人数为50-9-16-7-4=14,数据2出现了16次,出现次数最多,
所以植树株数的众数是2;
条形统计图补充如图所示.
(2)因为植3株的人数为50-9-16-7-4=14(人),且所占总人数比例:14÷50=28%,
∴“植树3株”对应扇形的圆心角的度数为:28%×360=100.8(度);
(3)∵该班植树株数的平均数=(9×1+16×2+14×3+7×4+4×5)÷50=2.62,
植树株数超过该班植树株数平均数的人数有:14+7+4=25(人),
∴概率=$\frac{25}{50}$=0.5.
答:植树株数超过该班植树株数平均数的概率是0.5.
点评 本题主要考查了条形统计图以及概率的计算,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.解题时注意:一组数据按顺序排列后,中间的那两个数的平均数或中间的那个数叫做中位数;概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.化简(1-$\frac{2x-1}{{x}^{2}}$)÷(1-$\frac{1}{{x}^{2}}$)的结果为( )
| A. | $\frac{x-1}{x+1}$ | B. | $\frac{x+1}{x-1}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系? 推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)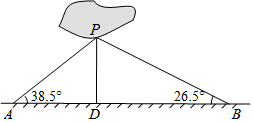 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)


