题目内容
15.若实数x满足x2-$2\sqrt{2}$x-1=0,则${x^2}+\frac{1}{x^2}$=10.分析 根据x2-$2\sqrt{2}$x-1=0,可以求得$x-\frac{1}{x}$的值,从而可以得到${x^2}+\frac{1}{x^2}$的值,本题得以解决.
解答 解:∵x2-$2\sqrt{2}$x-1=0,
∴$x-2\sqrt{2}-\frac{1}{x}=0$,
∴$x-\frac{1}{x}=2\sqrt{2}$,
∴$(x-\frac{1}{x})^{2}=8$,
即${x}^{2}-2+\frac{1}{{x}^{2}}=8$,
∴${x}^{2}+\frac{1}{{x}^{2}}=10$,
故答案为:10.
点评 本题考查代数式求值,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.北京时间2016年2月11日23点30分,科学家宣布:人类首次直接探测到了引力波,印证了爱因斯坦100年前的预言,引力波探测器LIGO的主要部分是两个互相垂直的长臂,每个臂长4000米,数据4000用科学记数法表示为( )
| A. | 0.4×103 | B. | 0.4×104 | C. | 4×103 | D. | 4×104 |
3. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{8\sqrt{13}}{13}$ | D. | $\frac{12\sqrt{13}}{13}$ |

 如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )
如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )



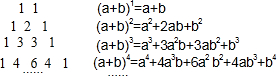 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):