题目内容
6.已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:
按照上述规律排下去,那么第10行从左边数第5个数等于-50.
分析 设第n行的第1个数的绝对值为an,根据数列排列方式找出部分an的值,根据数值的变化找出变化规律“an=$\frac{n(n-1)}{2}$+1”,依此规律再结合数列中所有奇数为正,偶数为负即可得出结论.
解答 解:设第n行的第1个数的绝对值为an,
观察,发现规律:a1=1,a2=|-2|=2=a1+1,a3=|-4|=4=a2+2,a4=7=a3+3,a5=11=a4+4,…,
∴an=an-1+n-1.
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+1+2+…+n-1=$\frac{n(n-1)}{2}$+1.
当n=10时,a10=$\frac{10×(10-1)}{2}$+1=46,
∴第10行从左边数第5个数的绝对值为:46+(5-1)=50.
又∵该数列中奇数为正,偶数为负,
∴第10行从左边数第5个数为-50.
故答案为:-50.
点评 本题考查了规律型中得数字的变化类,解题的关键是找出规律第n行第一个数的绝对值为$\frac{n(n-1)}{2}$+1.本题属于中档题,难度不大,解决该题型题目时,罗列出前几行的第一个数的绝对值,根据数值的变化找出变化规律是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.一次数学测试,某小组五名同学的成绩如下表(有1个数据被遮盖)
那么这五名同学成绩的方差是2分2.
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 平均成绩 |
| 成绩 | 91 | 89 | ★ | 90 | 92 | 90 |
11.某大学生对新一代无人机的续航时间进行7次测试,一次性飞行时间(单位:分钟)分别为20、22、21、26、25、22、25.则这7次测试续航时间的中位数是( )
| A. | 22或25 | B. | 25 | C. | 22 | D. | 21 |
18.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
16.对下列生活现象的解释其数学原理运用错误的是( )
| A. | 把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 | |
| B. | 木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理 | |
| C. | 将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”的原理 |
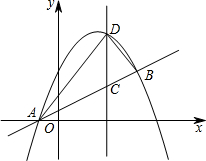 如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD. 如图所示的图形是由7个完全相同的小正方形组成的立体图形,则这个立体图形的左视图是( )
如图所示的图形是由7个完全相同的小正方形组成的立体图形,则这个立体图形的左视图是( )


