题目内容
7.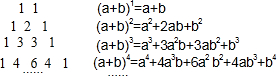 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):请依据上述规律,写出(x-$\frac{2}{x}$)2016展开式中含x2014项的系数是-4032.
分析 首先确定x2014是展开式中第几项,根据杨辉三角即可解决问题.
解答 解:(x-$\frac{2}{x}$)2016展开式中含x2014项的系数,
由(x-$\frac{2}{x}$)2016=x2016-2016•x2015•($\frac{2}{x}$)+…
可知,展开式中第二项为-2016•x2015•($\frac{2}{x}$)=-4032x2014,
∴(x-$\frac{2}{x}$)2016展开式中含x2014项的系数是-4032,
故答案为-4032.
点评 本题考查整式的混合运算、杨辉三角等知识,解题的关键是灵活运用杨辉三角解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.一次数学测试,某小组五名同学的成绩如下表(有1个数据被遮盖)
那么这五名同学成绩的方差是2分2.
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 平均成绩 |
| 成绩 | 91 | 89 | ★ | 90 | 92 | 90 |
18.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
16.对下列生活现象的解释其数学原理运用错误的是( )
| A. | 把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 | |
| B. | 木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理 | |
| C. | 将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”的原理 |
 如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.
如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.
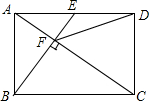 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论: