题目内容
4.在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.

分析 (1)由旋转得到∠BAC=∠BAD,而DF⊥AC,从而得出∠ABC=45°,最后判断出△ABC是等腰直角三角形;
(2)①由旋转得到∠BAC=∠BAD,再根据∠DAF=∠DBA,从而求出∠FAD=∠BAC=∠BAD=60°,最后判定△AFD≌△BED,即可;
②根据题意画出图形,先求出角度,得到△ABD是顶角为36°的等腰三角形,再用相似求出,$\frac{AD}{BD}=\frac{1+\sqrt{5}}{2}$,最后判断出△AFD∽△BED,代入即可.
解答 解:(1)由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB,
(2)①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=$\frac{1}{3}$×180°=60°,
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
$\left\{\begin{array}{l}{∠F=∠BED=90°}\\{∠FAD=∠BED}\\{AD=BD}\end{array}\right.$,
∴△AFD≌△BED,
∴AF=BE,
②如图,
由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD-AG=AD-BG=AD-BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴$\frac{BD}{AD}=\frac{DG}{DB}$.
∵DG=AD-BD,
∴$\frac{BD}{AD}=\frac{AD-BD}{BD}$=$\frac{AD}{BD}$-1,
∴$\frac{BD}{AD}=\frac{AD}{BD}$-1,
∴$\frac{1}{\frac{AD}{BD}}=\frac{AD}{BD}$-1,
∴1=($\frac{AD}{BD}$)2-$\frac{AD}{BD}$
即($\frac{AD}{BD}$)2-$\frac{AD}{BD}$-1=0,
∴$\frac{AD}{BD}=\frac{1+\sqrt{5}}{2}$,
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴$\frac{AD}{BD}=\frac{AF}{BE}$,
∴AF=$\frac{AD}{BD}×BE$=$\frac{1+\sqrt{5}}{2}$x.
点评 此题是几何变换综合题,主要考查了,等腰直角三角形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,旋转的性质,解本题的关键是求出顶角为36°的等腰三角形的腰与底的比值,也是本题的难点.

 阅读快车系列答案
阅读快车系列答案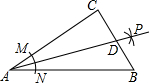 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )| A. | 15 | B. | 30 | C. | 45 | D. | 60 |
| A. | 把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 | |
| B. | 木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理 | |
| C. | 将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”的原理 |
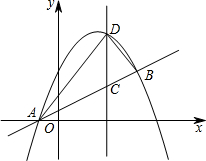 如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.