题目内容
16．下面两个多位数1397139，6842684，…都是按照如下方法得到的：从左边起，将第1位数字乘以3，若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位．再对第2位数字再进行如上操作，得到第3位数字…，后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是2时，若按如上操作得到一个多位数，则这个多位数前50位数字之和是（ ）| A． | 242 | B． | 248 | C． | 254 | D． | 258 |
分析 由题意可得第2位数字是6，第3位数字是8，第4位数字是4，第5位数字是2，即可得四次一循环，由50÷4=12…2，即可求得答案．
解答 解：∵第1位数字是2，
∴第2位数字是6，第3位数字是8，第4位数字是4，第5位数字是2，
∴四次一循环，
∴50÷4=12…2，
∴这个多位数第49位与50位数字分别是2，6，
∴12×（2+6+8+4）+2+6=248．
故选B．
点评 此题考查了数字变化类问题．注意根据题意得到这个多位数是四次一循环是关键．
练习册系列答案
相关题目
4．
如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，且DE∥BC，EF∥AB，若AD=2BD，则$\frac{CF}{CB}$的值为（ ）
如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，且DE∥BC，EF∥AB，若AD=2BD，则$\frac{CF}{CB}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |
已知：如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1，y2=ax2-ax-1（其中a为常数，且a＞0）．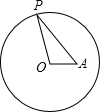
如图，点A在半径为3的⊙O内，OA=$\sqrt{3}$，P为⊙O上一点，当∠OPA取最大值时，PA的长等于$\sqrt{6}$．
如图，将边长为4的正方形ABCD折叠，使B点落在边AD上，记作B′（不与A、D重合）、EF为折痕，设AB′=x．
如图，以扇形AOB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），∠AOB=45°．现从$-2，-\frac{3}{2}，-1，-\frac{1}{2}，0，\frac{1}{2}$中随机选取一个数记为a，则a的值既使得抛物线$y=\frac{1}{2}{x^2}+a$与扇形AOB的边界有公共点，又使得关于x的方程$\frac{ax+1}{x-2}=-1$的解是正数的概率是$\frac{1}{6}$．