Question

1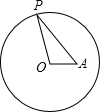．如图，点A在半径为3的⊙O内，OA=$\sqrt{3}$，P为⊙O上一点，当∠OPA取最大值时，PA的长等于$\sqrt{6}$．

Answer 1

分析 当PA⊥OA时，PA取最小值，∠OPA取得最大值，然后在直角三角形OPA中利用勾股定理求PA的值即可．

解答 解：在△OPA中，当∠OPA取最大值时，OA取最大值，
∴PA取最小值，
又∵OA、OP是定值，
∴PA⊥OA时，PA取最小值；
在直角三角形OPA中，OA=$\sqrt{3}$，OP=3，
∴PA=$\sqrt{{3}^{2}-（\sqrt{3}）^{2}}$=$\sqrt{6}$．
故答案为：$\sqrt{6}$．

点评 本题考查了解直角三角形．解答此题的关键是找出“当PA⊥OA时，PA取最小值”即“PA⊥OA时，∠OPA取最大值”这一隐含条件．