题目内容
8. 如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x.
如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x.(1)用x的代数式表示BE的长;
(2)设四边形BCFE的面积为S,求S关于x的函数关系式,并写出定义域.
分析 (1)设BE=B'E=y,在RT△AEB′中利用勾股定理即可得出答案.
(2)作FM⊥AB垂足为M,由△ABB′≌△MFE得AB′=EM=x得出CF=BM=BE-EM,求出四边形BCFE的面积为S即可.
解答 解:(1)设BE=B'E=y,
因此有:x2+(4-y)2=y2,
整理得:y=$\frac{1}{8}$x2+2;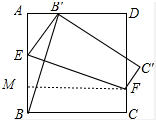
(2)如图作FM⊥AB垂足为M,
∵四边形EB′C′F是由四边形EBCF翻折得到,
∴EF⊥BB′,
∴∠ABB′+∠BEF=90°,∠BEF+∠MFE=90°,
∴∠ABB′=∠MFE,
∵A四边形BCD是正方形,
∴∠MBC=∠C=∠BMF=90°,
∴四边形MFCB是矩形,
∴MF=BC=AB,
在△ABB′和△MFE中,
$\left\{\begin{array}{l}{∠ABB′=∠MFE}\\{AB=MF}\\{∠A=∠EMF}\end{array}\right.$,
∴△ABB′≌△MFE,
∴ME=AB′=x,
∴FC=BM=EB-EM=$\frac{1}{8}$x2-x+2,
∴S=$\frac{1}{2}$($\frac{1}{8}{x}^{2}+2+\frac{1}{8}{x}^{2}-x+2$)•4=$\frac{1}{2}{x}^{2}$-2x+8(0<x<4).
点评 此题考查了翻折变换、正方形的性质、全等三角形的判定和性质、梯形的面积的求法等知识,利用翻折不变性是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
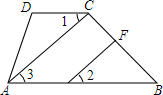 如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程.
如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程.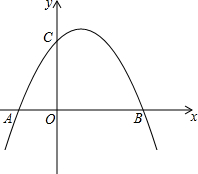 如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.
如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C. 如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$.
如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$. 如图,该图形由6个完全相同的小正方形排列而成.
如图,该图形由6个完全相同的小正方形排列而成.