题目内容
4．
如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，且DE∥BC，EF∥AB，若AD=2BD，则$\frac{CF}{CB}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |
分析 先由AD=2BD，求得BD：AB的比，再由DE∥BC，根据平行线分线段成比例定理，可得CE：AC=BD：AB，然后由EF∥AB，根据平行线分线段成比例定理，可得CF：CB=CE：AC，则可求得答案．
解答 解：∵AD=2BD，
∴BD：AB=1：3，
∵DE∥BC，
∴CE：AC=BD：AB=1：3，
∵EF∥AB，
∴CF：CB=CE：AC=1：3．
故选B．
点评 此题考查了平行线分线段成比例定理．此题比较简单，注意掌握比例线段的对应关系是解此题的关键．
练习册系列答案
相关题目
8．
已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（ ）
已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（ ）| A． | ac＞0 | |
| B． | 方程ax2+bx+c=0的两根是x1=-1，x2=3 | |
| C． | 不等式ax2+bx+c＜0的解集是-1＜x＜3 | |
| D． | 当x＞0时，y随x的增大而减小 |
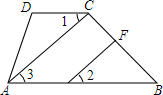如图，在四边形ABCD中，∠BCD+∠B=180°，AC⊥CB于C，EF⊥CB于F，∠1和∠2相等吗？请完成下面的说理过程．
如图，正△ABC的边长是4，分别以点B，C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当2$\sqrt{2}$≤r≤4时，S的取值范围是2π-4≤x≤$\frac{16}{3}$π-4$\sqrt{3}$．
如图，在矩形ABCD中，AB=8，BC=12，点E为BC的中点．连接AE，将△ABE沿AE折叠，点B落在点F处，连接CF，现将△CEF绕点E顺时针旋转α角（其中0°≤α≤180°）得到△EC1F1，旋转过程中，直线C1F1分别交射线EC、射线AE于点M、N，当EM=EN时，则CM=6-$\frac{12\sqrt{5}}{5}$．