题目内容
15.有四个式子:①$\sqrt{18}=3\sqrt{2}$;②$\sqrt{9}=±3$;③${(\sqrt{5}+1)^2}=6$;④3a3•2a2=6a6,从这四个式子中随机抽取一个,抽到的式子不正确的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
分析 根据概率的公式计算即可.
解答 解:抽到的式子不正确的有3个,即;②$\sqrt{9}=±3$;③${(\sqrt{5}+1)^2}=6$;④3a3•2a2=6a6,
所以从这四个式子中随机抽取一个,抽到的式子不正确的概率是$\frac{3}{4}$,
故选C.
点评 此题考查概率问题,关键是根据概率公式解答.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
6.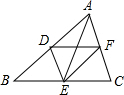 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )| A. | AB⊥AC | B. | AB=AC | C. | AB=BC | D. | AC=BC |
10. 如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )
 如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“炮”位于点( )| A. | (-2,-1) | B. | (0,0) | C. | (1,-2) | D. | (-1,1) |
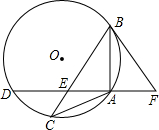 已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.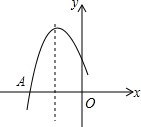 二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )
二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )