题目内容
11. 如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )
如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 24 |
分析 根据三角形中位线定理,可得ED=FG=$\frac{1}{2}$BC,GD=EF=$\frac{1}{2}$AO,进而求出四边形DEFG的周长.
解答 解:∵BD,CE是△ABC的中线,
∴ED∥BC且ED=$\frac{1}{2}$BC,
∵F是BO的中点,G是CO的中点,
∴FG∥BC且FG=$\frac{1}{2}$BC,
∴ED=FG=$\frac{1}{2}$BC=$\frac{7}{2}$,
同理GD=EF=$\frac{1}{2}$AO=$\frac{5}{2}$,
∴四边形DEFG的周长为$\frac{7}{2}$+$\frac{5}{2}$+$\frac{7}{2}$+$\frac{5}{2}$=12.
故选B.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形中位线的性质定理,为证明线段相等和平行提供了依据.

练习册系列答案
相关题目
19.当x取何值时,|x-1|+|x-2|+…+|x-2021|有最小值.( )
| A. | 1 | B. | 1010 | C. | 1011 | D. | 2020 |
 如图,每个圆的半径都为2cm,求图中阴影部分的面积.
如图,每个圆的半径都为2cm,求图中阴影部分的面积.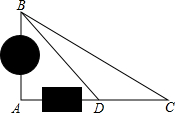 如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)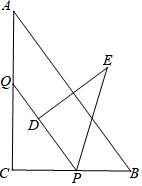 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上. 如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.