题目内容
19.当x取何值时,|x-1|+|x-2|+…+|x-2021|有最小值.( )| A. | 1 | B. | 1010 | C. | 1011 | D. | 2020 |
分析 此题可以用数形结合来解题:x为数轴上的一点,|x-1|+|x-2|+|x-3|+…|x-2021|表示:点x到数轴上的2021个点(1、2、3、…、2021)的距离之和,进而分析得出最小值为:|1011-1|+|1011-2|+|1011-3|+…|1011-2021|求出即可.
解答 解:在数轴上,要使点x到两定点的距离和最小,
则x在两点之间,最小值为两定点为端点的线段长度(否则距离和大于该线段);
所以:当1≤x≤2021时,|x-1|+|x-2021|有最小值2021;
当2≤x≤2021时,|x-2|+|x-2021|有最小值2021;
…
当x=1011时,|x-1011|有最小值0.
综上,当 x=1011时,|x-1|+|x-2|+|x-3|+…|x-2021|能够取到最小值,
最小值为:|1011-1|+|1011-2|+|1011-3|+…|1011-2021|
=1010+1009+…+0+1+2+…+1010
=1011×1010
=1021110.
故选:C.
点评 此题主要考查了绝对值的性质以及利用数形结合求最值问题,利用已知得出x=1011时,|x-1|+|x-2|+|x-3|+…|x-2021|能够取到最小值是解题关键.

练习册系列答案
相关题目
14.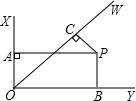 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\sqrt{6}$-2 | D. | 2$\sqrt{3}$-3 |
9. 如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ的度数( )
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ的度数( )
 如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ的度数( )
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ的度数( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
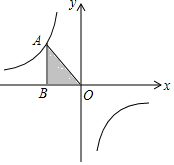 如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2.
如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2. 如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
 如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )
如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )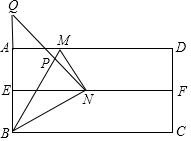 如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.
如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.