题目内容
我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)= .(其中n为自然数).
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=
考点:规律型:数字的变化类
专题:
分析:根据观察,可得规律:等式左边是n个相邻的奇数相加,等式的右边是n的平方,根据规律,可得答案.
解答:解:我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=n2,
故答案为:n2.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=n2,
故答案为:n2.
点评:本题考查了数字的变化类,观察、发现规律是解题关键.

练习册系列答案
相关题目
 如图,在矩形ABCD中,把点B沿AF对折,使点B落在CD边上的E点,若AB=10,AC=8,求FE的长.
如图,在矩形ABCD中,把点B沿AF对折,使点B落在CD边上的E点,若AB=10,AC=8,求FE的长.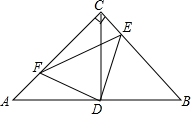 如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD
如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD 如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5
如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5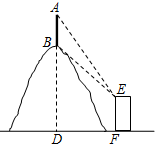 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)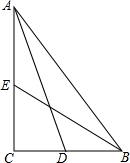 如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=
如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=