题目内容
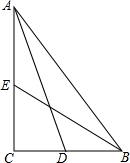 如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=
如图,在△ABC中,∠C=90°,AD,BE分别为边BC,AC上的中线,且AD=| 40 |
考点:勾股定理
专题:计算题
分析:设BC=a,AC=b,在直角三角形ACD与直角三角形BEC中,利用勾股定理列出关于a与b的方程,联立求出a与b的值,即可确定出三角形面积.
解答:解:设BC=a,AC=b,
在Rt△ACD中,根据勾股定理得:AD2=AC2+CD2=40,即40=
a2+b2;
在Rt△BEC中,根据勾股定理得:BE2=BC2+CE2=25,即25=a2+
b2;
联立解得:a=4,b=6,
∴S△ABC=
×4×6=12.
在Rt△ACD中,根据勾股定理得:AD2=AC2+CD2=40,即40=
| 1 |
| 4 |
在Rt△BEC中,根据勾股定理得:BE2=BC2+CE2=25,即25=a2+
| 1 |
| 4 |
联立解得:a=4,b=6,
∴S△ABC=
| 1 |
| 2 |
点评:此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)= .(其中n为自然数).
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=
代数式a=
,4xy,
,a,2014,
a2b,-
中,单项式的个数有( )
| 1 |
| 2a |
| a+b |
| 3 |
| 1 |
| 2 |
| 3mn |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
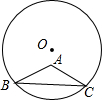 △ABC中,AB=AC=5,BC=8,半径为
△ABC中,AB=AC=5,BC=8,半径为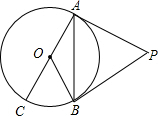 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.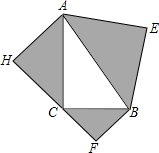 如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为 如图已知∠α,根据三角函数的定义求sinα,cosα,tanα.
如图已知∠α,根据三角函数的定义求sinα,cosα,tanα.