题目内容
18.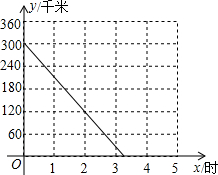 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.(1)求y关于x的关系式;
(2)已知乙车以60km/h的速度匀速行驶.设行驶过程中,两车相距的路程s(km).请直按写出s关于x的表达式;
(3)乙车按(2)中的状态行驶,试问当x(h)为多少时两车相遇?当x(h)为多少时两车相距100km?
分析 (1)根据速度=路程÷时间可求出甲车的速度,再根据甲车距B城高速公路入口处的距离=300-甲车的速度×行驶时间,即可得出y关于x的关系式;
(2)根据时间=路程÷速度求出甲车到达B城的时间,再分0≤x≤$\frac{10}{3}$和$\frac{10}{3}$<x≤5两种情况寻找s关于x的表达式;
(3)分别求出当s=0和s=100时的x值,此题得解.
解答 解:(1)甲车的速度为(300-120)÷2=90(km/h),
∴y关于x的关系式为y=300-90x.
(2)甲车到达B城的时间为300÷90=$\frac{10}{3}$(h),
当0≤x≤$\frac{10}{3}$时,s=|300-(90+60)x|=|300-150x|;
当$\frac{10}{3}$<x≤5时,s=60x.
∴s关于x的表达式为s=$\left\{\begin{array}{l}{|300-150x|(0≤x≤\frac{10}{3})}\\{60x(\frac{10}{3}<x≤5)}\end{array}\right.$.
(3)当s=|300-150x|=0时,x=2;
当s=|300-150x|=100时,x=$\frac{4}{3}$或x=$\frac{8}{3}$.
答:当x=2时两车相遇,当x=$\frac{4}{3}$或x=$\frac{8}{3}$时两车相距100km.
点评 本题考查了一次函数的应用以及一次函数图象上点的坐标特征,解题的关键是:(1)根据数量关系,列出函数关系式;(2)分0≤x≤$\frac{10}{3}$和$\frac{10}{3}$<x≤5两种情况寻找s关于x的表达式;(3)分别求出当s=0和s=100时的x值.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
18.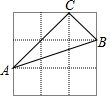 如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
 如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
6.已知二次函数y=x2-(m+1)x-5m(m为常数).在-1≤x≤3的范围内至少有一个x的值使y≥2,则m的取值范围是( )
| A. | m≤0 | B. | 0≤m≤$\frac{1}{2}$ | C. | m≤$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
8.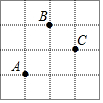 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )| A. | (1,2) | B. | (2,3) | C. | (3,2) | D. | (2,1) |
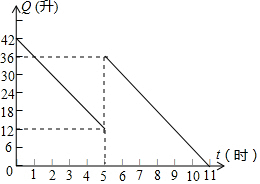 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.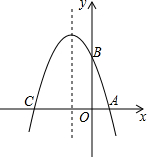 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.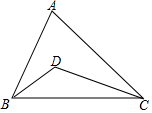 如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.
如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.