题目内容
15.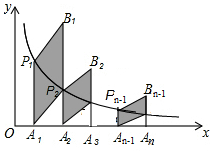 如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)
如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)
分析 根据反比例函数图象上点的坐标特征求得点P1、P2的纵坐标,由平行四边形对边平行且相等,求得点B1的纵坐标是y2+y1、B2的纵坐标是y3+y2、B3的纵坐标是y4+y3,据此可以推知点Bn的纵坐标是:yn+1+yn=$\frac{3}{n+1}$+$\frac{3}{n}$=$\frac{6n+3}{n(n+1)}$.
解答 解:∵点P1(1,y1),P2(2,y2)在反比例函数y=$\frac{3}{x}$的图象上,
∴y1=3,y2=$\frac{3}{2}$,
∴P1A1=y1=3,
又∵四边形A1P1B1P2,是平行四边形,
∴P1A1=B1P2=3,P1A1∥B1P2 ,
∴点B1的纵坐标是:y2+y1=$\frac{3}{2}$+3=$\frac{9}{2}$;
同理求得,点B2的纵坐标是:y3+y2=1+$\frac{3}{2}$=$\frac{5}{2}$;
点B3的纵坐标是:y4+y3=$\frac{3}{4}$+1=$\frac{7}{4}$;
…
∴点Bn的纵坐标是:yn+1+yn=$\frac{3}{n+1}$+$\frac{3}{n}$=$\frac{6n+3}{n(n+1)}$.
故答案是:$\frac{9}{2}$,$\frac{6n+3}{n(n+1)}$.
点评 本题考查了平行四边形的性质、反比例函数图象上点的坐标特征、反比例函数的图象的综合应用.解答此题的关键是根据平行四边形的对边平行且相等,求得点Bn的纵坐标为yn+1+yn.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
6.已知二次函数y=x2-(m+1)x-5m(m为常数).在-1≤x≤3的范围内至少有一个x的值使y≥2,则m的取值范围是( )
| A. | m≤0 | B. | 0≤m≤$\frac{1}{2}$ | C. | m≤$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
5. 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 5cm |
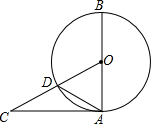 如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=120°.
如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=120°.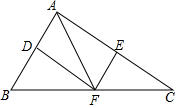 如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且BC=2AF.
如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且BC=2AF.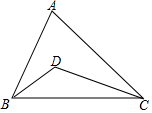 如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.
如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.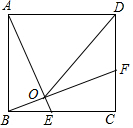 如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.
如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.