题目内容
5. 如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G.
如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G.(1)若CG=3,求BH的长;
(2)若BF,GF的长分别是一元二次方程x2-7x+6=0的两根,求正方形ABCD的面积;
(3)求证:$\frac{B{E}^{2}}{B{C}^{2}}=\frac{EH}{AH}$.
分析 (1)由BF垂直于AE,且CG与AE平行,得到CG垂直于BF,进而得到一对直角相等,再利用同角的余角相等得到一对角相等,根据四边形ABCD为正方形,得到一对边相等,利用AAS得到三角形ABH与三角形BCG全等,利用全等三角形的对应边相等得到BH=CG,即可求出BH的长;
(2)求出方程的解确定出BF与GF的长,由BF-GF求出BG的长,利用相似三角形对应边成比例求出CG的长,利用勾股定理求出正方形边长,即可确定出面积;
(3)由全等三角形对应边相等得到AH=BG,由三角形BEH与三角形BCG相似,由相似得比例,两边平方后等量代换即可得证.
解答 (1)解:∵正方形ABCD,
∴AB=BC,∠ABC=90°,
∴∠ABH+∠CBG=90°,
∵BF⊥AE,CG∥AE,
∴CG⊥AE,
∴∠CBG+∠BCG=90°,
∴∠ABH=∠BCG,
在△ABH和△BCG中,
$\left\{\begin{array}{l}{∠AHB=∠BGC=90°}\\{∠ABH=∠BCG}\\{AB=BC}\end{array}\right.$,
∴△ABH≌△BCG(AAS),
∴BH=CG=3;
(2)方程x2-7x+6=0变形得:(x-1)(x-6)=0,
解得:x=1或x=6,
∵BF,GF的长分别是一元二次方程x2-7x+6=0的两根,且BF>GF,
∴BF=6,GF=1,
∴BG=BF-GF=6-1=5,
在Rt△BCF中,CG⊥BF,
∴△BCG∽△CFG,
∴CG2=BG•GF=5,
∴根据勾股定理得:BC2=BG2+GC2=25+5=30,
则正方形的面积为30;
(3)∵HE∥BG,
∴△BEH∽△BCG,
∴$\frac{BE}{BC}$=$\frac{BH}{BG}$,即$\frac{B{E}^{2}}{B{C}^{2}}$=$\frac{B{H}^{2}}{B{G}^{2}}$,
∵AH=BG,BH2=AH•HE,
∴$\frac{B{E}^{2}}{B{C}^{2}}$=$\frac{B{H}^{2}}{B{G}^{2}}$=$\frac{AH•HE}{A{H}^{2}}$=$\frac{HE}{AH}$.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,全等三角形的判定与性质,解一元二次方程-因式分解法,勾股定理,熟练掌握相似三角形的判定与性质是解本题的关键.

 寒假学与练系列答案
寒假学与练系列答案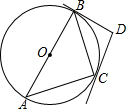 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )| A. | 15° | B. | 30° | C. | 40° | D. | 45° |
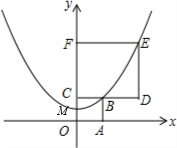 如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则$\frac{FE}{CB}$的值为1+$\sqrt{2}$.
如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则$\frac{FE}{CB}$的值为1+$\sqrt{2}$.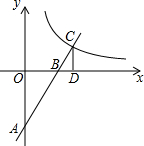 如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.
如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.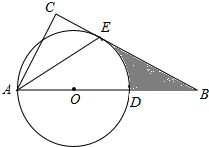 如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.
如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.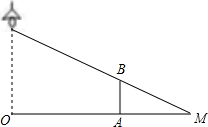 如图,路灯垂直照射在地面的位置为点O,小华(用线段AB表示)站在离路灯不远的A处,在路灯的照射(中心投影)下,可形成小华的影子是线段AM.
如图,路灯垂直照射在地面的位置为点O,小华(用线段AB表示)站在离路灯不远的A处,在路灯的照射(中心投影)下,可形成小华的影子是线段AM.