题目内容
13.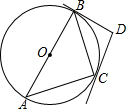 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )| A. | 15° | B. | 30° | C. | 40° | D. | 45° |
分析 首先连接OC,由BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,利用四边形内角和定理,即可求得∠AOC的度数,再利用圆周角定理,即可求得答案.
解答  解:连接OC,
解:连接OC,
∵BD、CD分别是过⊙O上点B、C的切线,
∴OB⊥BD,OC⊥CD,
∵∠BDC=100°,
∴在四边形OBDC中,∠BOC=360°-90°-90°-100°=80°,
∴∠A=$\frac{1}{2}$∠BOC=40°.
故选C.
点评 此题考查了切线的性质、圆周角定理以及四边形的内角和.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.
如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.
 如图,半径为1的⊙P的圆心在抛物线y=-x2+4x-3上运动,当⊙P在x轴相切时,圆心P的坐标是(2,1),(2+$\sqrt{2}$,-1),(2-$\sqrt{2}$,-1).
如图,半径为1的⊙P的圆心在抛物线y=-x2+4x-3上运动,当⊙P在x轴相切时,圆心P的坐标是(2,1),(2+$\sqrt{2}$,-1),(2-$\sqrt{2}$,-1).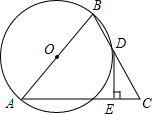 已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.
已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点. 如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G.
如图,在正方形ABCD中,E是BC上一点,连接AE,作BF⊥AE,垂足为点H,交CD于点F.作CG∥AE,交BF于点G. 已知:如图BD、CE是△ABC的外角平分线,AD⊥BD,AE⊥CE,△ABC的周长为2,求DE的长.
已知:如图BD、CE是△ABC的外角平分线,AD⊥BD,AE⊥CE,△ABC的周长为2,求DE的长.