题目内容
3.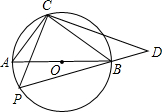 如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为( )
如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为( )| A. | 36 | B. | 24 | C. | 18 | D. | 12 |
分析 利用圆周角定理得到∠ACB=90°,再利用勾股定理计算出AC=$\frac{18}{5}$,BC=$\frac{24}{5}$,则S△ACB=$\frac{216}{25}$,接着证明Rt△PDC∽Rt△ABC,利用相似三角形的性质得到$\frac{{S}_{△PDC}}{{S}_{△ABC}}$=($\frac{PC}{AC}$)2,由于当PC为直径时最大,S△PDC最大,所以S△PDC的最大值为$\frac{216}{25}$×($\frac{6}{\frac{18}{5}}$)2=24.
解答 解:∵AB为直径,
∴∠ACB=90°,
在Rt△ACB中,设BC=4x,AC=3x,
∴AB=5x,
∴5x=6,解得x=$\frac{6}{5}$,
∴AC=$\frac{18}{5}$,BC=$\frac{24}{5}$,
∴S△ACB=$\frac{1}{2}$×$\frac{18}{5}$×$\frac{24}{5}$=$\frac{216}{25}$,
∵∠A=∠P,
∴Rt△PDC∽Rt△ABC,
∴$\frac{{S}_{△PDC}}{{S}_{△ABC}}$=($\frac{PC}{AC}$)2,
∴S△PDC=$\frac{216}{25}$×($\frac{PC}{\frac{18}{5}}$)2,
∴当PC最大时,S△PDC最大,
而PC的最大值为6,
∴S△PDC的最大值为$\frac{216}{25}$×($\frac{6}{\frac{18}{5}}$)2=24.
故选B.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;在利用相似三角形的性质时,主要利用相似比计算线段的长.也考查了圆周角定理.

| A. | (-1,3) | B. | (-1,-3) | C. | (3,1) | D. | (1,3) |
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x≠0 |
| A. | 3 | B. | 4 | C. | 5 | D. | ±5 |
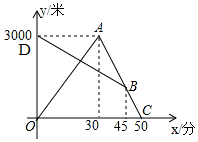 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法: