题目内容
20.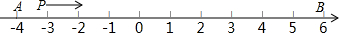 如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).
如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).(1)求t=2时点P表示的有理数;
(2)求点P是AB的中点时t的值;
(3)在点P由点A到点B的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)在点P由点B到点A的返回过程中,点P表示的有理数是多少(用含t的代数式表示).
分析 (1)根据P点的速度,有理数的加法,可得答案;
(2)根据两点间的距离公式,可得AB的长度,根据路程除以速度,可得时间;
(3)根据速度乘以时间等于路程,可得答案;
(4)根据速度乘以时间等于路程,可得答案.
解答 解:(1)点P表示的有理数为-4+2×2=0;
(2)6-(-4)=10,
10÷2=5,
5÷2=2.5,
(10+5)÷2=7.5.
故点P是AB的中点时t=2.5 或7.5;
(3)在点P由点A到点B的运动过程中,点P与点A的距离为2t;
(4)在点P由点B到点A的返回过程中,点P表示的有理数是6-2(t-5)=16-2t.
点评 本题考查了数轴,利用了速度与时间的关系,分类讨论是解题关键.

练习册系列答案
相关题目
10.如果函数 y=kx+k-1的图象不经过第二象限,那么k的取值范围是( )
| A. | k>0 | B. | 0<k<1 | C. | k>1 | D. | 0≤k≤1 |
11.若(x-1)0=1,则( )
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x≠0 |
8. 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;
②小华的速度是小明速度的2.5倍;
③a=24;④b=480.
其中正确的是( )
 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:①小华先到达青少年宫;
②小华的速度是小明速度的2.5倍;
③a=24;④b=480.
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
8.据报道,2016年初我国网民规模达719 000 000人,将这个数用科学记数法表示为( )
| A. | 7.19×109 | B. | 7.19×108 | C. | 71.9×107 | D. | 0.719×109 |
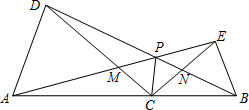 如图,C为线段AB上的任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证:△ACE≌△DCB.
如图,C为线段AB上的任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证:△ACE≌△DCB.