题目内容
2.计算与化简:(1)$\sqrt{36×256}$
(2)$\sqrt{12{x}^{3}}$
(3)$\frac{1}{4}$$\sqrt{12a}$×3$\sqrt{3a}$
(4)2$\sqrt{xy}$×$\frac{1}{3}$$\sqrt{\frac{1}{x}}$
(5)$\frac{4xy}{\sqrt{2x}}$
(6)$\sqrt{12x}$÷$\frac{2}{5}$$\sqrt{y}$
(7)$\frac{2\sqrt{{x}^{2}y}}{3\sqrt{xy}}$
(8)$\frac{a+2}{2\sqrt{a+2}}$.
分析 (1)直接利用二次根式的性质化简求出答案;
(2)直接利用二次根式的性质化简求出答案;
(3)直接利用二次根式的乘法运算法则求出答案;
(4)直接利用二次根式的乘法运算法则求出答案;
(5)直接利用二次根式的性质化简求出答案;
(6)直接利用二次根式的除法运算法则求出答案;
(7)直接利用二次根式的性质化简求出答案;
(8)直接利用二次根式的性质化简求出答案.
解答 解:(1)$\sqrt{36×256}$=$\sqrt{36}$×$\sqrt{256}$=6×16=96;
(2)$\sqrt{12{x}^{3}}$=2x$\sqrt{3x}$;
(3)$\frac{1}{4}$$\sqrt{12a}$×3$\sqrt{3a}$
=$\frac{1}{4}$×2$\sqrt{3a}$×3$\sqrt{3a}$
=$\frac{3}{2}$×3a
=$\frac{9a}{2}$;
(4)2$\sqrt{xy}$×$\frac{1}{3}$$\sqrt{\frac{1}{x}}$
=$\frac{2}{3}$×$\sqrt{xy•\frac{1}{x}}$
=$\frac{2}{3}$$\sqrt{y}$;
(5)$\frac{4xy}{\sqrt{2x}}$=$\frac{4xy\sqrt{2x}}{2x}$=2y$\sqrt{2x}$;
(6)$\sqrt{12x}$÷$\frac{2}{5}$$\sqrt{y}$
=2$\sqrt{3x}$×$\frac{5}{2}$$\sqrt{\frac{1}{y}}$
=$\frac{5\sqrt{3xy}}{y}$;
(7)$\frac{2\sqrt{{x}^{2}y}}{3\sqrt{xy}}$=$\frac{2\sqrt{x}}{3}$;
(8)$\frac{a+2}{2\sqrt{a+2}}$=$\frac{(\sqrt{a+2})^{2}}{2\sqrt{a+2}}$=$\frac{\sqrt{a+2}}{2}$.
点评 此题主要考查了二次根式的乘除运算以及二次根式的化简,正确掌握运算法则是解题关键.

| A. | (-1,3) | B. | (-1,-3) | C. | (3,1) | D. | (1,3) |
| A. | k>0 | B. | 0<k<1 | C. | k>1 | D. | 0≤k≤1 |
| A. | $\frac{9}{2}$$\sqrt{2}$ | B. | -$\frac{7}{2}$$\sqrt{2}$ | C. | $\frac{9}{\sqrt{2}}$ | D. | -$\frac{7}{\sqrt{2}}$ |
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x≠0 |
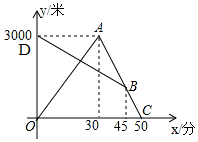 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: