题目内容
8.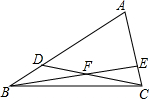 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
分析 可设S△ADF=m,根据题中条件可得出三角形的面积与边长之间的关系,进而用m表示出△AEF,求出m的值,进而可得四边形的面积.
解答 解:如图,连AF,设S△ADF=m,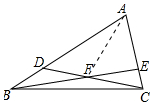
∵S△BDF:S△BCF=12:16=3:4=DF:CF,
则有$\frac{4}{3}$m=S△AEF+S△EFC,
S△AEF=$\frac{4}{3}$m-12,
而S△BFC:S△EFC=16:12=4:3=BF:EF,
又∵S△ABF:S△AEF=BF:EF=4:3,
而S△ABF=m+S△BDF=m+12,
∴S△ABF:S△AEF=BF:EF=4:3=(m+12):($\frac{4}{3}$m-12),
解得m=36.
S△AEF=36,
SADEF=S△AEF+S△ADF=36+36=72.
故答案为:72.
点评 本题主要考查了三角形的面积计算问题,能够利用三角形的性质进行一些简单的计算.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
18. 为了让书籍开拓学生的视野,陶冶学生的情操,某中学开展课外阅读活动.为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
为了让书籍开拓学生的视野,陶冶学生的情操,某中学开展课外阅读活动.为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
(1)将频数和频率分布表补全,直接写出上面的频数a、b、c和频率m、n、p的值;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
 为了让书籍开拓学生的视野,陶冶学生的情操,某中学开展课外阅读活动.为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
为了让书籍开拓学生的视野,陶冶学生的情操,某中学开展课外阅读活动.为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:| 组别 | 分组 | 频数(人数) | 频率 |
| 1 | 10≤t<30 | a | 0.16 |
| 2 | 30≤t<50 | 20 | m |
| 3 | 50≤t<70 | b | 0.28 |
| 4 | 70≤t<90 | 6 | n |
| 5 | 90≤t<110 | c | p |
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
20.$\sqrt{{3}^{2}}$的立方根是( )
| A. | $\root{3}{3}$ | B. | $\root{3}{9}$ | C. | 2 | D. | 3 |
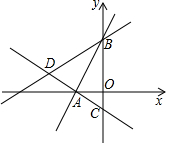 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
 如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.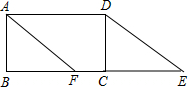 如图,点E是矩形ABCD边延长线上一点,且AB=6,BC=10,CE=8,过点A作DE的平行线交BC于点F.
如图,点E是矩形ABCD边延长线上一点,且AB=6,BC=10,CE=8,过点A作DE的平行线交BC于点F.