题目内容
19.有红、黄两个盒子,红盒子中装有编号分别为1、2、3、4的四个红球,黄盒子中装有编号为1、2、3的三个黄球.甲、乙两人玩摸球游戏,游戏规则为:甲从红盒子中每次摸出一个小球,乙从黄盒子中每次摸出一个小球,若两球编号之和为奇数,则甲胜,否则乙胜.(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?请说明理由.
分析 (1)首先画树状图,然后根据树状图即可求得甲获胜的概率;
(2)根据树状图,求得甲、乙获胜的概率,然后比较概率,即可求得这个游戏规则对甲、乙双方是否公平.
解答 解:(1)画树状图得:
∴一共有12种等可能的结果,两球编号之和为奇数有6种情况,
∴P(甲胜)=$\frac{6}{12}=\frac{1}{2}$;
(2)公平.
∵P(乙胜)=$\frac{6}{12}=\frac{1}{2}$,
∴P(甲胜)=P(乙胜),
∴这个游戏规则对甲、乙双方公平;
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在-3,2,-1,3这四个数中,比-2小的数是( )
| A. | -3 | B. | 2 | C. | -1 | D. | 3 |
14.2016年9月15日,我国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.大约经过10分钟后,成功进入远地点350000米的初始轨道.将数据350000用科学记数法可表示为( )
| A. | 35×104 | B. | 350×103 | C. | 3.5×105 | D. | 0.35×106 |
 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC. 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.
如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.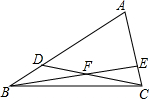 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.