题目内容
16.如果正方形ABCD的边长为1,圆A与以CD为半径的圆C相交,那么圆A的半径R的取值范围是$\sqrt{2}$-1<R<$\sqrt{2}$+1.分析 根据题意画出图形,利用当圆A与以CD为半径的圆C相外切以及当圆A与以CD为半径的圆C相内切,分别求出半径,即可确定半径R的取值范围.
解答 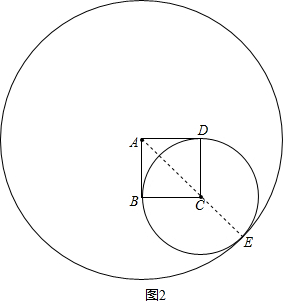
 解:∵正方形ABCD的边长为1,
解:∵正方形ABCD的边长为1,
∴如图1,当圆A与以CD为半径的圆C相外切,
∵AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=CD=FC=1,
AF+FC=AC,
∴AF=AC-FC=$\sqrt{2}$-1,
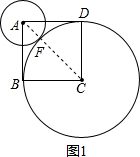
如图2,当圆A与以CD为半径的圆C相内切,
∵AC═$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=CD=EC=1,
AC+EC=AE,
∴AE=AC+EC=$\sqrt{2}$+1,
综上所述:圆A的半径R的取值范围为:$\sqrt{2}$-1<R<$\sqrt{2}$+1,
故答案为:$\sqrt{2}$-1<R<$\sqrt{2}$+1.
点评 此题主要考查了相切两圆的性质以及正方形的性质,根据已知进行分类讨论得出是解题关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7.在-3,2,-1,3这四个数中,比-2小的数是( )
| A. | -3 | B. | 2 | C. | -1 | D. | 3 |
5.某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每分钟收费b元,如果某人打一次该长途电话被收费m元,则这次长途电话的时间是( )
| A. | $\frac{m-a}{b}$分钟 | B. | $\frac{m}{a+b}$分钟 | C. | $\frac{m-a+b}{b}$分钟 | D. | $\frac{m-a-b}{b}$分钟 |
6.下列四个点中,有三个点在同一反比例函数y=$\frac{k}{x}$的图象上,则不在这个函数图象上的点是( )
| A. | (5,1) | B. | (-1,5) | C. | (-3,-$\frac{5}{3}$) | D. | ($\frac{5}{3}$,3) |
 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.
如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数. 某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题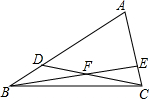 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.