题目内容
 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AB的长是
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AB的长是考点:含30度角的直角三角形
专题:
分析:由垂直平分线的性质可得AD=CD,∠CDB=2∠A=60°,在Rt△BCD中可求出CD的长,则可得到AB的长.
解答:解:∵DE垂直平分斜边AC,
∴AD=CD,
∵∠A=30°,
∴∠BDC=2∠A=60°,
∴∠DCB=30°,
∴CD=AD=2BD=2,
∴AB=AD+BD=2+1=3,
故答案为:3.
∴AD=CD,
∵∠A=30°,
∴∠BDC=2∠A=60°,
∴∠DCB=30°,
∴CD=AD=2BD=2,
∴AB=AD+BD=2+1=3,
故答案为:3.
点评:本题主要考查垂直平分线的性质和含30°角的直角三角形的性质,由条件得到∠DCB=30°是解题的关键.

练习册系列答案
相关题目
在△ABC中,∠C-30°=∠A+∠B,则△ABC是( )
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、有一个角30°的等腰三角形 |
 如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=
如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=| k |
| x |
A、(-1,
| ||||
B、(-2,
| ||||
C、(-
| ||||
D、(-3,
|
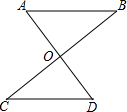 已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证:
已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证: 如图,△ABC中,∠C=90°,AD为角平分线.若BC=5,BD=2,则点D到边AB的距离为
如图,△ABC中,∠C=90°,AD为角平分线.若BC=5,BD=2,则点D到边AB的距离为