题目内容
9.已知x2-5x+1=0,则$\frac{{x}^{2}}{{x}^{4}+3{x}^{2}+1}$的值是$\frac{1}{26}$.分析 先根据题意得出x2=5x-1,再根据分式混合运算的法则进行计算即可.
解答 解:∵x2-5x+1=0,
∴x2=5x-1,
∴原式=$\frac{5x-1}{(5x-1)^{2}+3{x}^{2}+1}$
=$\frac{5x-1}{{25x}^{2}+1-10x+3{x}^{2}+1}$
=$\frac{5x-1}{{28x}^{2}-10x+2}$
=$\frac{5x-1}{28(5x-1)-10x+2}$
=$\frac{5x-1}{26(5x-1)}$
=$\frac{1}{26}$.
故答案为:$\frac{1}{26}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
17.若a<b,则下列不等式中错误的是( )
| A. | a+5<b+5 | B. | -4a>-4b | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | a(x2+2)>b(x2+2) |
14.下列计算正确的是( )
| A. | a-(2b-3c)=-(a+2b-3c) | B. | x3-b和-x3-b互为相反数 | ||
| C. | 当x<0时,|3x-x|=-2x | D. | 1×(-1)+2÷(-1)-(-1)=0 |
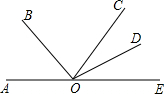 如图,点A、O、E在同一直线上,∠AOB=40°,OD平分∠COE,∠BOC=3∠COD+10°,求∠BOC的度数.
如图,点A、O、E在同一直线上,∠AOB=40°,OD平分∠COE,∠BOC=3∠COD+10°,求∠BOC的度数.