题目内容
8.在平面直角坐标系中,已知点A(-2,2)、B(3,4)、C(0,-1),直线y=kx+b过点C且与线段AB有交点,则k的取值范围是k≤-$\frac{3}{2}$或k≥$\frac{5}{3}$.分析 已知直线y=kx+b与y轴的交点C的坐标,利用待定系数法求出直线AC、BC的解析式,然后根据直线与线段AB有交点,则k值小于AC的k值,或大于BC的k值,然后根据此范围进行选择即可.
解答  解:直线y=kx+b与y轴的交点坐标为(0,-1),
解:直线y=kx+b与y轴的交点坐标为(0,-1),
设直线AC的解析式为y=mx+n,
则$\left\{\begin{array}{l}{-2m+n=2}\\{n=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{3}{2}}\\{n=-1}\end{array}\right.$.
所以直线AC的解析式为y=-$\frac{3}{2}$x-1,
设直线BC的解析式为y=ex+f,
则$\left\{\begin{array}{l}{3e+f=4}\\{f=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{e=\frac{5}{3}}\\{f=-1}\end{array}\right.$.
所以直线BC的解析式为y=$\frac{5}{3}$x-1,
若直线y=kx-2与线段AB有交点,则k的取值范围是k≤-$\frac{3}{2}$或k≥$\frac{5}{3}$,
故答案为:k≤-$\frac{3}{2}$或k≥$\frac{5}{3}$.
点评 本题考查了两直线相交的问题,由待定系数法求一次函数的解析式,求出两直线的解析式是解题的关键.

练习册系列答案
相关题目
18.已知圆的半径为R,这个圆的内接正六边形的面积为( )
| A. | $\frac{3\sqrt{3}}{4}$R2 | B. | $\frac{3\sqrt{3}}{2}$R2 | C. | 6R2 | D. | 1.5R2 |
15. 如图,点B、C的坐标分别是(2,m),(8,4m-1),那么点A的坐标是( )
如图,点B、C的坐标分别是(2,m),(8,4m-1),那么点A的坐标是( )
 如图,点B、C的坐标分别是(2,m),(8,4m-1),那么点A的坐标是( )
如图,点B、C的坐标分别是(2,m),(8,4m-1),那么点A的坐标是( )| A. | (-3,-2) | B. | (-2,-1) | C. | (-1,-2) | D. | (-4,-2) |
17.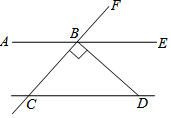 如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
 如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
 如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)
如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)