题目内容
18.已知圆的半径为R,这个圆的内接正六边形的面积为( )| A. | $\frac{3\sqrt{3}}{4}$R2 | B. | $\frac{3\sqrt{3}}{2}$R2 | C. | 6R2 | D. | 1.5R2 |
分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,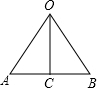
∠AOB=60°,OA=OB=R,
则△OAB是正三角形,
∵OC=OA•sin∠A=$\frac{\sqrt{3}}{2}$R,
∴S△OAB=$\frac{1}{2}$AB•OC=$\frac{\sqrt{3}}{4}$R2,
∴正六边形的面积为6×$\frac{\sqrt{3}}{4}$R2=$\frac{3\sqrt{3}}{2}$R2,
故选B.
点评 本题考查的正多边形和圆,理解正六边形被半径分成六个全等的等边三角形是解答此题的关键.

练习册系列答案
相关题目
8.-$\frac{\sqrt{3}}{3}$的绝对值是( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
10.关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m≥-$\frac{5}{4}$ | B. | m≤-$\frac{5}{4}$ | C. | m<-$\frac{5}{4}$ | D. | m>-$\frac{5}{4}$ |
8.在平面直角坐标系中,已知点A(-2,2)、B(3,4)、C(0,-1),直线y=kx+b过点C且与线段AB有交点,则k的取值范围是k≤-$\frac{3}{2}$或k≥$\frac{5}{3}$.
9.下列式子中,不是二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{a^2}$ | C. | $\sqrt{a}$ | D. | $\sqrt{\frac{1}{3}}$ |
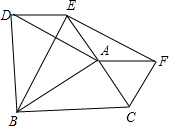 如图,?ADEF两边AD、AF向外作等边△ADB、△AFC,连接EB、EC、BC.
如图,?ADEF两边AD、AF向外作等边△ADB、△AFC,连接EB、EC、BC.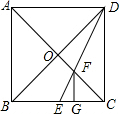 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.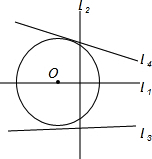 如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )