题目内容
11.如图:已知△ABC中,∠ABC的n等分线与∠ACB的n等分线分别相交于G1,G2,G3,…,Gn-1,试猜想:∠BGn-1C与∠A的关系.(其中n是不小于2的整数)首先得到:当n=2时,如图1,∠BG1C=90°+$\frac{1}{2}$∠A,
当n=3时,如图2,∠BG2C=60°+$\frac{2}{3}$∠A,…
如图3,猜想∠BGn-1C=$\frac{180°}{n}$+$\frac{n-1}{n}$∠A.…
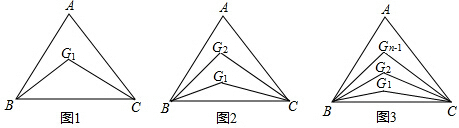
分析 当n=2时,用∠A表示出∠G1BC+∠G1CB的度数,再由三角形内角和定理即可得出∠BG1C的度数;当n=3时,用∠A表示出∠G2BC+∠G2CB的度数,再由三角形内角和定理即可得出∠BG2C的度数,根据n=2与n=3的结论可得出猜想.
解答 解:∵当n=2时,∠G1BC+∠G1CB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A),
∴∠BG1C=180°-(∠G1BC+∠G1CB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A;
∵当n=3时,∠G2BC+∠G2CB=$\frac{2}{3}$(∠ABC+∠ACB)=$\frac{2}{3}$(180°-∠A),
∴∠BG2C=180°-$\frac{2}{3}$(∠ABC+∠ACB)=180°-$\frac{2}{3}$(180°-∠A)=60°+$\frac{2}{3}$∠A.
由n=2,n=3可知,∠BGn-1C=$\frac{180°}{n}$+$\frac{n-1}{n}$∠A.
故答案为:90°+$\frac{1}{2}$∠A,60°+$\frac{2}{3}$∠A,$\frac{180°}{n}$+$\frac{n-1}{n}$∠A.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
1.下列从左到右的变形中,属于因式分解的是( )
| A. | (x+y)(x-2y)=x2-xy+y2 | B. | 3x2-x=x(3x-1) | ||
| C. | (a-b)2=(a-b)(a-b) | D. | m2-n2=(m-n)2 |
6.4的平方根是( )
| A. | ±16 | B. | 2 | C. | ±2 | D. | ±$\sqrt{2}$ |
16.一元二次方程x2+3=2$\sqrt{3}$x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的有理根 | ||
| C. | 有两个相等的无理根 | D. | 没有实数根 |
3. 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )| A. | 65° | B. | 25° | C. | 30° | D. | 15° |
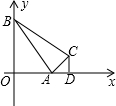 如图,已知A(3,0),B(0,4),C(4,2),作CD⊥x轴于D,连接AB,BC,AC,证明:△ABC∽△ACD.
如图,已知A(3,0),B(0,4),C(4,2),作CD⊥x轴于D,连接AB,BC,AC,证明:△ABC∽△ACD.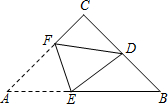 如图1,在△ABC中,CA=CB=4,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么BE的值为$\frac{7\sqrt{2}}{3}$.
如图1,在△ABC中,CA=CB=4,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么BE的值为$\frac{7\sqrt{2}}{3}$.