题目内容
7.有甲乙丙三名射击运动员,要从中选拔一名参加射击比赛,环数如下:甲:10,10,9,10,9,9,9,9,9,9;
乙:10,10,10,9,10,8,8,10,10,8;
丙:10,9,8,10,8,9,10,9,9,9.
根据以上环数,应选谁参加比赛?
分析 分别计算出三人的平均数和方差,进行比较,根据平均数和方差的意义作出判断即可.
解答 解:甲的平均数:$\frac{1}{10}$(10+10+9+10+9+9+9+9+9+9)=9.3,
乙的平均数:$\frac{1}{10}$(10+10+10+9+10+8+8+10+10+8)=9.3,
丙的平均数:$\frac{1}{10}$(10+9+8+10+8+9+10+9+9+9)=9.1,
甲的方差:$\frac{1}{10}$[(10-9.3)2×3+(9-9.3)2×7]=0.21,
乙的方差:$\frac{1}{10}$[(10-9.3)2×6+(9-9.3)2+(8-9.3)2×3]=0.81,
∵甲、乙的平均数大于丙的平均数,甲的方差小于乙的方差,
故选甲参加比赛.
点评 本题考查的是方差的计算和意义,掌握方差的计算公式和方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元; 乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
按上述优惠条件,若贝贝第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品各多少件?
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
16.一元二次方程x2+3=2$\sqrt{3}$x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的有理根 | ||
| C. | 有两个相等的无理根 | D. | 没有实数根 |
17. 如图,在方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△能作出( )
如图,在方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△能作出( )
 如图,在方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△能作出( )
如图,在方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△能作出( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
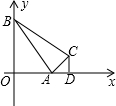 如图,已知A(3,0),B(0,4),C(4,2),作CD⊥x轴于D,连接AB,BC,AC,证明:△ABC∽△ACD.
如图,已知A(3,0),B(0,4),C(4,2),作CD⊥x轴于D,连接AB,BC,AC,证明:△ABC∽△ACD.