题目内容
计算下列各题:
(1)(ab2)2•(-5a3b)÷(-ab);
(2)3a(2a2-9a+3)-4a(2a-1);
(3)计算:20032-2002×2004;
(4)已知2x-y=10,求[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值.
(1)(ab2)2•(-5a3b)÷(-ab);
(2)3a(2a2-9a+3)-4a(2a-1);
(3)计算:20032-2002×2004;
(4)已知2x-y=10,求[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值.
考点:整式的混合运算,代数式求值,平方差公式
专题:
分析:(1)先算乘方,再算乘除;
(2)先算乘法,再合并同类项即可;
(3)先根据平方差公式进行计算,再合并同类项即可;
(4)先算乘法,再合并同类项,最后算除法,代入求出即可.
(2)先算乘法,再合并同类项即可;
(3)先根据平方差公式进行计算,再合并同类项即可;
(4)先算乘法,再合并同类项,最后算除法,代入求出即可.
解答:解:(1)原式=a2b4•(-5a3b)÷(-ab)
=5a4b4;
(2)原式=6a3-27a2+9a-8a2+4a
=6a3-35a2+13a;
(3)原式=20032-(2003-1)×(2003+1)
=20032-20032+1
=1;
(4)[(x2+y2)-(x-y)2+2y(x-y)]÷4y
=(x2+y2-x2+2xy-y2+2xy-2y2)÷4y
=(4xy-2y2)÷4y
=x-
y,
当2x-y=10时,原式=10÷2=5.
=5a4b4;
(2)原式=6a3-27a2+9a-8a2+4a
=6a3-35a2+13a;
(3)原式=20032-(2003-1)×(2003+1)
=20032-20032+1
=1;
(4)[(x2+y2)-(x-y)2+2y(x-y)]÷4y
=(x2+y2-x2+2xy-y2+2xy-2y2)÷4y
=(4xy-2y2)÷4y
=x-
| 1 |
| 2 |
当2x-y=10时,原式=10÷2=5.
点评:本题考查了整式的混合运算的应用,主要考查学生的计算能力和化简能力,题目比较好,难度适中.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
一筐苹果4千克,增加
后,列出的算式为( )
| 1 |
| 2 |
A、4+
| ||
B、4×(1+
| ||
| C、4÷(1+) | ||
D、4×(1-
|
一组数据中的每个数都加10,则①平均数加10;②中位数不变;③极差加10;④方差不变.其中正确的说法有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
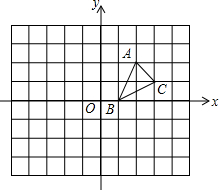 如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)
如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)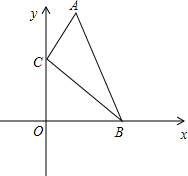 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.