题目内容
已知直线y=x+5与y=-
x;
(1)求两直线的交点坐标;
(2)求两直线与x轴所围成的三角形面积;
(3)在同一直角坐标系中画出它们的图象.
| 3 |
| 2 |
(1)求两直线的交点坐标;
(2)求两直线与x轴所围成的三角形面积;
(3)在同一直角坐标系中画出它们的图象.
考点:两条直线相交或平行问题
专题:
分析:(1)联立方程组,求方程组的解即可得.
(2)分别求出两直线与x轴的交点坐标,从而求出两点之间的距离,再联立两解析式求出交点坐标,然后根据三角形的面积公式列式计算即可得解.
(3)根据网格结构确定出直线经过的两个点的位置,然后利用两点法作出函数图象即可;
(2)分别求出两直线与x轴的交点坐标,从而求出两点之间的距离,再联立两解析式求出交点坐标,然后根据三角形的面积公式列式计算即可得解.
(3)根据网格结构确定出直线经过的两个点的位置,然后利用两点法作出函数图象即可;
解答:解:(1)联立
,
解得
.
所以两直线的交点坐标为(-2,3).
(2)令y=0,则x+5=0,
解得x=-5,
所以直线y=x+5与x轴的交点A坐标为(-5,0),
∵直线y=-
x经过原点,
∴两点间的距离为AO=5,
∵两直线的交点坐标为(-2,3),
所以,两直线与x轴围成的三角形的面积=
×5×3=
.
(3)如图所示

|
解得
|
所以两直线的交点坐标为(-2,3).
(2)令y=0,则x+5=0,
解得x=-5,
所以直线y=x+5与x轴的交点A坐标为(-5,0),
∵直线y=-
| 3 |
| 2 |
∴两点间的距离为AO=5,
∵两直线的交点坐标为(-2,3),
所以,两直线与x轴围成的三角形的面积=
| 1 |
| 2 |
| 15 |
| 2 |
(3)如图所示

点评:本题考查了两线相交的问题,利用联立两直线的解析式求交点坐标是常用的方法,需要熟练掌握.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.
已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.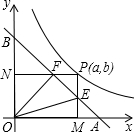 如图,在平面直角坐标系中,直线y=-x+
如图,在平面直角坐标系中,直线y=-x+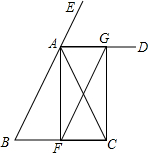 如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.