题目内容
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.(1)求证:
①△AEF≌△DEB;
②四边形ADCF是平行四边形;
(2)若AB=AC,∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论.
考点:正方形的判定,全等三角形的判定与性质,平行四边形的判定
专题:
分析:(1)①根据AAS证△AFE≌△DBE;
②利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”证得结论;
(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据正方形的判定推出即可.
②利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”证得结论;
(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据正方形的判定推出即可.
解答:(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
②由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)四边形ADCF是正方形.理由如下:
证明:∵在△ABC中,AB=AC,∠BAC=90°,AD是斜边BC上的中线,
∴AD⊥BC,AD=
BC=DC,
∴平行四边形ADCF是正方形.
(注:其他证明方法参照以上评分标准给分.)
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
|
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
②由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)四边形ADCF是正方形.理由如下:
证明:∵在△ABC中,AB=AC,∠BAC=90°,AD是斜边BC上的中线,
∴AD⊥BC,AD=
| 1 |
| 2 |
∴平行四边形ADCF是正方形.
(注:其他证明方法参照以上评分标准给分.)
点评:本题考查了全等三角形的性质和判定,平行四边形的判定,菱形的判定的应用,主要考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙I是△ABC的内切圆,已知∠A=50°.
如图,⊙I是△ABC的内切圆,已知∠A=50°.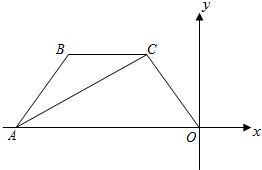 如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1,
如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1,