题目内容
9. 已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
分析 作AM⊥BC于M,交DG于N,设BC=acm,BC边上的高为hcm,DG=DE=xcm,根据题意得出方程组求出BC和AM,再由平行线得出△ADG∽△ABC,由相似三角形对应高的比等于相似比得出比例式,即可得出结果.
解答 解:作AM⊥BC于M,交DG于N,如图所示: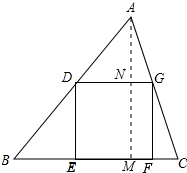
设BC=acm,BC边上的高为hcm,DG=DE=xcm,
根据题意得:$\left\{\begin{array}{l}{a+h=100}\\{\frac{1}{2}ah=1200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=60}\\{h=40}\end{array}\right.$,或$\left\{\begin{array}{l}{a=40}\\{h=60}\end{array}\right.$(不合题意,舍去),
∴BC=60cm,AM=h=40cm,
∵DG∥BC,
∴△ADG∽△ABC,
∴$\frac{AN}{AM}=\frac{DG}{BC}$,即$\frac{40-x}{40}=\frac{x}{60}$,
解得:x=24,
即加工成的正方形铁片DEFG的边长为24cm.
点评 本题考查了方程组的解法、相似三角形的运用;熟练掌握方程组的解法,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若方程组$\left\{\begin{array}{l}{3x+y=1+3a}\\{x+3y=1-a}\end{array}\right.$的解满足x+y=0,则a的值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 无法确定 |
17.某车间有28名工人生产螺丝与螺母,每人每天生产螺丝12个或螺母18个,现有x名工人生产螺丝,恰好每天生产的螺丝和螺母按2:1配套,为求x,列方程为( )
| A. | 12x=18(28-x) | B. | 2×12x=18(28-x) | C. | 2×18x=12(28-x) | D. | 12x=2×18(28-x) |
14.下列一元一次方程中,解为x=1的是( )
| A. | 4x-1=3x | B. | 2x-2=3x+3 | C. | 3x+2=2x-1 | D. | 4x-3=3x-1 |
19. 如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
 如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )| A. | 6 | B. | 7 | C. | 8 | D. | 11 |