题目内容
8.请观察下列算式,找出规律并填空:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$则:
(1)第10个算式是$\frac{1}{10×11}$=$\frac{1}{10}-\frac{1}{11}$.
(2)第n个算式为$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
(3)根据以上规律解答下题:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2013×2014}$的值.
分析 (1)直接得出第10个算式为:$\frac{1}{10×11}$=$\frac{1}{10}$-$\frac{1}{11}$;
(2)直接得出第n个算式为:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(3)分别将各算式的值代入,最后化简得出结果.
解答 解:(1)第10个算式是:$\frac{1}{10×11}$=$\frac{1}{10}$-$\frac{1}{11}$;
故答案为:$\frac{1}{10×11}$,$\frac{1}{10}-\frac{1}{11}$;
(2)第n个算式为:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
故答案为:$\frac{1}{n(n+1)}$,$\frac{1}{n}-\frac{1}{n+1}$;
(3)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2013×2014}$,
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$,
=1-$\frac{1}{2014}$,
=$\frac{2013}{2014}$.
点评 本题是数字类的规律题,此类题除了计算准确外,还要认真观察已知所给的式子,有什么关系,大胆猜想,仔细分析,利用特别的方法进行计算,并得出相应的规律.

练习册系列答案
相关题目
13. 如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
 如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )| A. | 40米 | B. | 30米 | C. | 20米 | D. | 10米 |
10.若向东走15米记为+15米,则向西走28米记为( )
| A. | -28米 | B. | +28米 | C. | 56米 | D. | -56米 |
20.一小商店一周的盈亏情况如表(亏为负),单位:元
(1)计算出小商店一周的盈亏情况;
(2)指出盈利最多一天的盈利额.
| 星期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 盈亏情况 | 128.3 | -25.6 | -15 | 27 | -7 | 36.5 | 98 |
(2)指出盈利最多一天的盈利额.
18.如图是2015年12月月历.
(1)如图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是x+1,x+7,x+8.
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2=128.
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2=128.
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
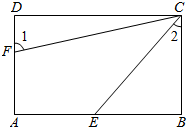 如图,已知四边形ABCD是平行四边形,并且∠A=∠D.
如图,已知四边形ABCD是平行四边形,并且∠A=∠D.