题目内容
13.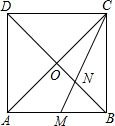 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )| A. | 4 | B. | 3 | C. | 2+$\sqrt{2}$ | D. | $\sqrt{2}+1$ |
分析 过点M作MF⊥AC于点F,根据角平分线的性质可知FM=BM,再由四边形ABCD为正方形,可得出∠FAM=45°,在直角三角形中用∠FAM的正弦值即可求出FM的长度,结合边的关系即可得出结论.
解答 解:过点M作MF⊥AC于点F,如图所示.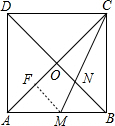
∵MC平分∠ACB,四边形ABCD为正方形,
∴∠CAB=45°,FM=BM.
在Rt△AFM中,∠AFM=90°,∠FAM=45°,AM=2,
∴FM=AM•sin∠FAM=$\sqrt{2}$.
AB=AM+MB=2+$\sqrt{2}$.
故选C.
点评 本题考查了正方形的性质以及角平分线的性质,解题的关键是在直角三角形中求出FM的长度.本题属于基础题,难度不大,解决该题型题目时,根据角平分的性质及正方形的特点找出边角关系,再利用解直角三角形的方法即可得以解决.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
3.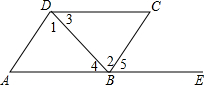 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠A+∠ABC=180° | C. | ∠A=∠5 | D. | ∠3=∠4 |
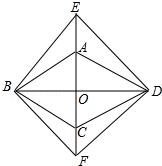 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.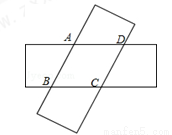
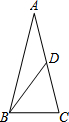 如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.
如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.