题目内容
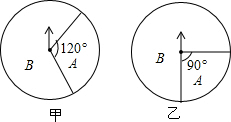
19．如图，有甲、乙两个构造完全相同的转盘均被分成A、B两个区域，甲转盘中A区域的圆心角是120°，乙转盘A区域的圆心角是90°，自由转动转盘，如果指针指向区域分界线则重新转动．（1）转动甲转盘一次，则指针指向A区域的概率$\frac{1}{3}$；
（2）自由转动两个转盘各一次，请用树状图或列表的方法，求出两个转盘同时指向B区域的概率？
分析 （1）A区域扇形的圆心角的度数与周角的度数的比即为指针指向A区域的概率；
（2）列表将所有等可能的结果列举出来即可求得同时指向B区域的概率．
解答 解：（1）∵A区域扇形的圆心角为120°，
∴转动甲转盘一次，则指针指向A区域的概率为$\frac{120}{360}$=$\frac{1}{3}$；
（2）表格或树状图：
| 甲 结果 乙 | A | B1 | B2 | B3 |
| A | （A，A） | （A，B1） | （A，B2） | （A，B3） |
| B1 | （B1，A） | （B1，B1） | （B1，B2） | （B1，B3） |
| B2 | （B2，A） | （B2，B1） | （B2，B2） | （B2，B3） |
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
9．5的绝对值是（ ）
| A． | 5 | B． | -5 | C． | $\frac{1}{5}$ | D． | -$\frac{1}{5}$ |
14．下列计算中，正确的是（ ）
| A． | x3•x3=2x6 | B． | （-2x3）2=-4x6 | C． | （x3）2=x5 | D． | x5÷x=x4 |
4．
如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（ ）
如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（ ）| A． | $\frac{6}{13}$ | B． | $\frac{5}{13}$ | C． | $\frac{4}{13}$ | D． | $\frac{3}{13}$ |
如图，在一块长为22米、宽为17米的矩形地面上，要修建一条长方形道路LMPQ及一条平行四边形道路RSTK，剩余部分种上草坪，使草坪面积为300平方米．若LM=RS=x米，则根据题意可列出方程为（22-x）（17-x）=300．