题目内容
 举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题:
举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题:(1)举例:要编织一块面积为2米2的矩形地毯,地毯的长x(米)与宽y(米)之间的函数关系是
| x | … |
| 1 |
| 2 | … | ||||
| y | … |
考点:反比例函数的应用
专题:
分析:(1)根据矩形的面积=长×宽知道xy=2,从而确定两个变量之间的关系并完成表格;
(2)根据xy=2可以得到y=
,从而作出图象并确定其三个性质.
(2)根据xy=2可以得到y=
| 2 |
| x |
解答:解:(1)∵xy=2,
∴x、y成反比例,
∴地毯的长x(米)与宽y(米)之间的函数关系是反比例函数关系;
(2)∵xy=2,
∴y=
(x>0),
图象为:

性质:1、图象位于一三象限;
2、在每一象限内y随着x的增大而减小;
3、图象可以无限接近两坐标轴,但永远不能与坐标轴相交.
∴x、y成反比例,
∴地毯的长x(米)与宽y(米)之间的函数关系是反比例函数关系;
| x | … |
| 1 |
| 2 | … | ||||
| y | 4 | 2 |
| 1 | … |
∴y=
| 2 |
| x |
图象为:

性质:1、图象位于一三象限;
2、在每一象限内y随着x的增大而减小;
3、图象可以无限接近两坐标轴,但永远不能与坐标轴相交.
点评:本题考查了反比例函数的应用,解题的关键是从实际问题中整理出反比例函数模型,接近生活实际,难度不大.

练习册系列答案
相关题目
 如图,梯子的各条横档互相平行,如果∠1=110°,则∠2的度数为( )
如图,梯子的各条横档互相平行,如果∠1=110°,则∠2的度数为( )| A、60° | B、70° |
| C、100° | D、110° |
 已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC.
已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC.
 如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积.
如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积. 直线y=mx+n如图所示,化简:|m-n|+
直线y=mx+n如图所示,化简:|m-n|+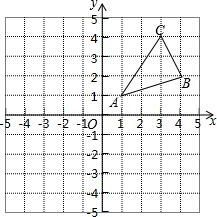 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)