题目内容
 已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC.
已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC.考点:全等三角形的判定与性质
专题:证明题
分析:根据三角形全等的性质与判断,可得EG=EF,根据角平分线的性质,可得EG=EH,再根据角平分线的性质,可得答案.
解答:解:过E点作EF⊥BC与F点,EG⊥AD于G,EH⊥AB于H,

∠EFC=∠EGD=∠AHE-90°,
由AD∥BC,得∠EDG=∠ECF,
由E是线段CD的中点,得ED=EC,
在△EDG和△ECF中,
,
∴△EDG≌△ECF(AAS),
∴EG=EF.
由角平分线的性质,得EG=EH,
∴EH=EF,
∴BE平分∠ABC.

∠EFC=∠EGD=∠AHE-90°,
由AD∥BC,得∠EDG=∠ECF,
由E是线段CD的中点,得ED=EC,
在△EDG和△ECF中,
|
∴△EDG≌△ECF(AAS),
∴EG=EF.
由角平分线的性质,得EG=EH,
∴EH=EF,
∴BE平分∠ABC.
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,角平分线的性质.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
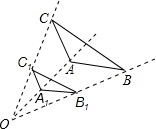 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,△A1B1C1面积是5,则△ABC的面积为( )
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,△A1B1C1面积是5,则△ABC的面积为( )| A、10 | B、20 | C、25 | D、50 |
 如图,矩形ABCD中,DE⊥AC,E为垂足,图中相似三角形共有(全等三角形除外)( )
如图,矩形ABCD中,DE⊥AC,E为垂足,图中相似三角形共有(全等三角形除外)( )| A、3对 | B、4对 | C、5对 | D、6对 |
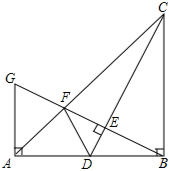 如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①
如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:① 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.
光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.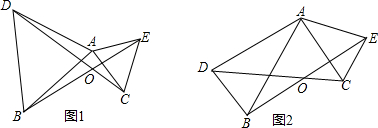
 举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题:
举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题: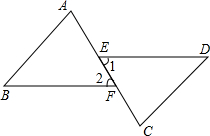 如图,已知∠A=∠C,AF=CE,DE∥BF,
如图,已知∠A=∠C,AF=CE,DE∥BF,