题目内容
△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，已知△ABC的面积是2，则△A′B′C′的面积是（ ）
| A、4 | B、6 | C、8 | D、12 |
考点：位似变换
专题：
分析：利用位似比得出三角形面积比，进而得出答案．
解答：解：∵△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，
∴
=
，
∵△ABC的面积是2，∴△A′B′C′的面积是：8．
故选：C．
∴
| S△ABC |
| S△A′B′C′ |
| 1 |
| 4 |
∵△ABC的面积是2，∴△A′B′C′的面积是：8．
故选：C．
点评：此题主要考查了位似变换，利用位似比得出面积比是解题关键．
练习册系列答案
相关题目
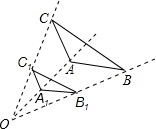如图，△ABC和△A1B1C1是以点O为位似中心的位似三角形，若C1为OC的中点，△A1B1C1面积是5，则△ABC的面积为（ ）| A、10 | B、20 | C、25 | D、50 |
如图，矩形ABCD中，DE⊥AC，E为垂足，图中相似三角形共有（全等三角形除外）（ ）| A、3对 | B、4对 | C、5对 | D、6对 |
举例是学习数学的常用方法，在学习函数时，张天同学举了一个生活中的函数关系实例，请你解答以下问题：