题目内容
 如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积.
如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积.考点:垂径定理的应用,勾股定理
专题:
分析:先根据弧长公式求出∠AOB的度数,故可得出△AOB是等腰直角三角形,再根据S有水部分=S⊙O-S弓形AB=S⊙O-S扇形OAB+S△AOB即可.
解答:解:设∠AOB=n°,
∵此管道的半径为54cm,水面以上部分的弧长为27πcm,
∴
=27π,解得n=90,
∴∠AOB=90°.
∵OA=OB,
∴△AOB是等腰直角三角形.
∴S有水部分=S⊙O-S弓形AB=S⊙O-S扇形OAB+S△AOB
=π×542-
+
×54×54
=2916π-729π-2458
=(2187π-2458)cm2.
∵此管道的半径为54cm,水面以上部分的弧长为27πcm,
∴
| nπ×54 |
| 180 |
∴∠AOB=90°.
∵OA=OB,
∴△AOB是等腰直角三角形.
∴S有水部分=S⊙O-S弓形AB=S⊙O-S扇形OAB+S△AOB
=π×542-
| 90π×542 |
| 360 |
| 1 |
| 2 |
=2916π-729π-2458
=(2187π-2458)cm2.
点评:本题考查的是垂径定理的应用,熟记弧长公式是解答此题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
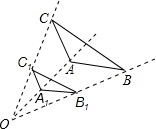 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,△A1B1C1面积是5,则△ABC的面积为( )
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,△A1B1C1面积是5,则△ABC的面积为( )| A、10 | B、20 | C、25 | D、50 |
下列说法中,正确的是( )
| A、斜边对应相等的两个直角三角形全等 |
| B、底边对应相等的两个等腰三角形全等 |
| C、面积相等的两个等边三角形全等 |
| D、面积相等的两个长方形全等 |
 举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题:
举例是学习数学的常用方法,在学习函数时,张天同学举了一个生活中的函数关系实例,请你解答以下问题: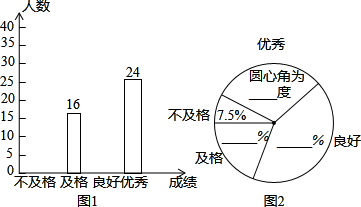
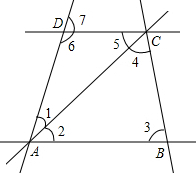 如图所示,从标有数字的角中找出:
如图所示,从标有数字的角中找出: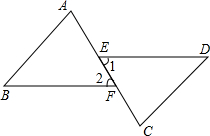 如图,已知∠A=∠C,AF=CE,DE∥BF,
如图,已知∠A=∠C,AF=CE,DE∥BF,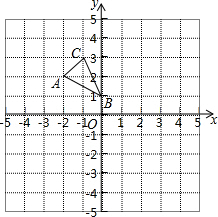 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).