题目内容
3．在一个不透明的盒子中装有3个形状大小完全一样的小球，上面分别有标号1，2，-1．（1）将球搅匀，从盒中一次取出两个小球，用树状图或列表的方法，求两标号互为相反数的概率；
（2）将球搅匀，摸出一个球将其标号记为k，放回后搅匀，再从中摸出一个球，将其标号记为b．则一次函数
y=kx+b的图象不经过第三象限的概率是$\frac{1}{3}$．
分析 （1）列表得到所有可能的结果即可求出两标号互为相反数的概率；
（2）列表得到所有可能的结果，要注意是不放回事件，即可求出一次函数y=kx+b的图象不经过第三象限的概率．
解答 解：（1）列表得：
| （2，1） | （-1，1） | |
| （1，2） | （-1，2） | |
| （1，-1） | （2，-1） |
所以两标号互为相反数的概率=$\frac{2}{6}$=$\frac{1}{3}$；
（2）列表得：
| （1，1） | （2，1） | （-1，1） |
| （1，2） | （2，2） | （-1，2） |
| （1，-1） | （2，-1） | （-1，-1） |
故答案为：$\frac{1}{3}$．
点评 此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
14．下列二次根式里，被开方数中各因式的指数都为1的是（ ）
| A． | $\sqrt{{x}^{2}{y}^{2}}$ | B． | $\sqrt{{x}^{2}+{y}^{2}}$ | C． | $\sqrt{（x+y）^{2}}$ | D． | $\sqrt{x{y}^{2}}$ |
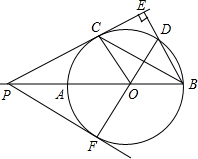如图，AB是⊙O的直径，延长BA至点P，过点P作⊙O的切线PC，切点为C，过点B向PC的延长线作垂线BE交该延长线于点E，BE交⊙O于点D，已知PA=1，PC=$\sqrt{3}$OC，
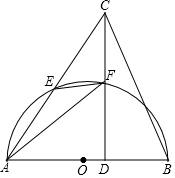如图，在△ABC中，CD⊥AB，垂足为点D．以AB为直径的半⊙O分别与
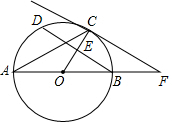如图，AB为⊙O的直径，CD为⊙O的弦，连接AC、BD，半径CO交BD于点E，过点C作切线，交AB的延长线于点F，且∠CFA=∠DCA．