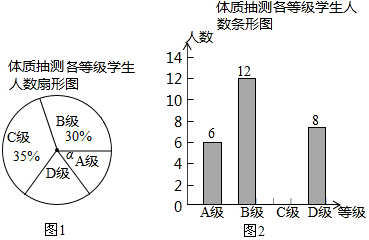
题目内容
15.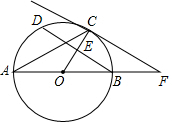 如图,AB为⊙O的直径,CD为⊙O的弦,连接AC、BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.
如图,AB为⊙O的直径,CD为⊙O的弦,连接AC、BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.(1)求证:OE⊥BD;
(2)若BE=2,CE=1
①求⊙O的半径;
②△ACF的周长是10+2$\sqrt{5}$.
分析 (1)根据切线的性质得到OC⊥CF,推出DB∥CF,根据平行线的性质即可得到结论;
(2)①设⊙O的半径为r,根据勾股定理求得结论;
②连接BC,根据勾股定理得到BC=$\sqrt{5}$,根据圆周角大家得到∠ACB=90°,根据勾股定理得到AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{5}$,由弦切角定理得到∠A=∠BCF,根据相似三角形的性质得到CF=2BF,BF=$\frac{5}{3}$,于是得到结论.
解答 (1)证明:∵CF是⊙O的切线,
∴OC⊥CF,
∴∠OCF=90°,
∵∠DCA=∠DBA,
∴∠DBA=∠CFA,
∴DB∥CF,
∴∠OEB=∠OCF=90°,
∴OE⊥DB;
(2)解:①设⊙O的半径为r,
∵CE=1,OE=r-1,
∵BE=2,
在Rt△BOE中,OB2=OE2+BE2,
∴r2=(r-1)2+22,
∴r=$\frac{5}{2}$,
∴⊙O的半径为$\frac{5}{2}$;
②连接BC,
∵CE=1,BE=2,
∴BC=$\sqrt{5}$,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{5}$,
∵CF是⊙O的切线,
∴∠A=∠BCF,
∵∠F=∠F,
∴△ACF∽△CBF,
∴$\frac{CF}{BF}=\frac{AC}{BC}$=2,
∴CF=2BF,
∵$\frac{CF}{AF}=\frac{BF}{CF}$,
∴CF2=AF•BF,
∴4BF2=(5+BF)•BF,
∴BF=$\frac{5}{3}$,
∴CF=$\frac{10}{3}$,AF=$\frac{20}{3}$,
∴△ACF的周长=AC+CF+AF=2$\sqrt{5}$+$\frac{10}{3}$+$\frac{20}{3}$=10+2$\sqrt{5}$.
故答案为:10+2$\sqrt{5}$.
点评 本题考查了切线的性质,圆周角定理,平行线的判定和性质,垂径定理,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

| 类别 | 进价 | 售价 |
| 甲 | 24 | 36 |
| 乙 | 33 | 48 |
①该商场购进甲、乙两种矿泉水各多少箱?
②全部售完500箱矿泉水,该商场共获得利润多少元?
(2)若设购进甲种矿泉水x箱,全部售完后商场共获得利润为y元.
③求出y与x之间的函数关系式;
④若商场进货部门拟定了两种进货方案:方案a:甲、乙两种矿泉水各进250箱,方案b:甲种矿泉水进300箱,乙种矿泉水进200箱,哪一种进货方案获利大?