题目内容
12.完成下列各题:(1)计算:2-1-(4-π)0+$\frac{1}{2}$
(2)解方程:$\frac{1}{x-2}$=$\frac{3}{2x+1}$.
分析 (1)根据实数的运算,可得答案;
(2)根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 (1)解:原式=$\frac{1}{2}$-1+$\frac{1}{2}$
=0;
(2)解:两边都乘以(x-2)(2x+1),得
3(x-2)=2x+1,
化简,得x=7
经检验:x=7是原分式方程的根.
点评 本题考查了解分式方程,利用等式的性质得出整式方程是解题关键,要检验分式方程的根.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
2.$\frac{1}{2}$是一个数的平方根,则这个数是( )
| A. | 1 | B. | 2 | C. | ±$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
 如图,在?ABCD中,∠BAD的平分线AE交DC于点E,若∠DAE=25°,求∠C、∠B的度数.
如图,在?ABCD中,∠BAD的平分线AE交DC于点E,若∠DAE=25°,求∠C、∠B的度数.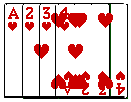 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.