题目内容
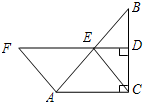 如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.
如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.(1)求证:四边形ACEF是平行四边形.
(2)若EC=2ED=2x,试求△ABC的面积与四边形ACEF面积的比值.
考点:平行四边形的判定与性质,勾股定理
专题:
分析:(1)由在Rt△ABC中,∠ACB=90°,AF=CE,点E为AB中点,易证得AF=CE=AE=EB,又由ED⊥BC,可证得∠1=∠2=∠F,证得CE∥AF,即可判定四边形ACEF是平行四边形.
(2)由EC=2ED=2x,可求得S△ABC=
AC•BC=
×2x×2
x=2
x2,S?ACEF=AC•CD=2x•
x=2
x2,即可证得△ABC的面积与四边形ACEF面积的比值为1.
(2)由EC=2ED=2x,可求得S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
解答: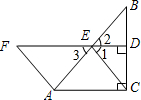 (1)证明:∵∠ACB=90°,点E为AB中点,
(1)证明:∵∠ACB=90°,点E为AB中点,
∴CE=AE=EB,
又∵AF=CE,
∴AF=CE=AE=EB,
又∵ED⊥BC,EB=EC,
∴∠1=∠2,
又∵∠2=∠3(对顶角相等),
∵AE=AF,
∴∠3=∠F,
∴∠1=∠2=∠F,
∴CE∥AF,
∵CE=AF,
∴四边形ACEF是平行四边形.
(2)解:由题意知:EC=2ED=2x,AC=2x,AB=4x,
在Rt△ABC中,∠ACB=90°,由勾股定理得:BC=
=
=2
x,
∴S△ABC=
AC•BC=
×2x×2
x=2
x2,
在Rt△CDE中,∠CDE=90°,由勾股定理可得:CD=
x,
∴S?ACEF=AC•CD=2x•
x=2
x2,
∴△ABC的面积与四边形ACEF面积的比值为1.
 (1)证明:∵∠ACB=90°,点E为AB中点,
(1)证明:∵∠ACB=90°,点E为AB中点,∴CE=AE=EB,
又∵AF=CE,
∴AF=CE=AE=EB,
又∵ED⊥BC,EB=EC,
∴∠1=∠2,
又∵∠2=∠3(对顶角相等),
∵AE=AF,
∴∠3=∠F,
∴∠1=∠2=∠F,
∴CE∥AF,
∵CE=AF,
∴四边形ACEF是平行四边形.
(2)解:由题意知:EC=2ED=2x,AC=2x,AB=4x,
在Rt△ABC中,∠ACB=90°,由勾股定理得:BC=
| AB2-AC2 |
| (4x)2+(2x)2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△CDE中,∠CDE=90°,由勾股定理可得:CD=
| 3 |
∴S?ACEF=AC•CD=2x•
| 3 |
| 3 |
∴△ABC的面积与四边形ACEF面积的比值为1.
点评:此题考查了平行四边形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
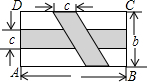 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是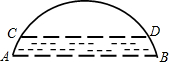 如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
 如图,直线AC与直线BD交于点O,∠AOB=2∠BOC,那么∠AOD=
如图,直线AC与直线BD交于点O,∠AOB=2∠BOC,那么∠AOD=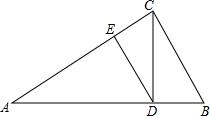 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.