题目内容
6. 如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.
如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.(1)若PB=PE,判断PB与⊙O的位置关系,并说明理由.
(2)若AC2=2AE2,求证:点E是AB的中点.
分析 (1)根据点A是$\widehat{CD}$的中点求出∠AFE=90°,求出∠OAE+∠AED=90°,根据∠OAE=∠OBA,∠PEB=∠PBE推出∠OB+∠PBE=90°,即∠OBP=90°,根据切线的判定得出即可;
(2)根据相似三角形的判定得出△ACE∽△ABC,得出比例式$\frac{AC}{AE}$=$\frac{AB}{AC}$,求出AB=2AE,即可得出答案.
解答 解:(1)PB与⊙O相切,
理由是:连接OA、OB,OA交CD于F,
∵点A是$\widehat{CD}$的中点,
∴OA⊥CD,
∴∠AFE=90°,
∴∠OAE+∠AED=90°,
∵OA=OB,PB=PE,
∴∠OAE=∠OBA,∠PEB=∠PBE,
∵∠AED=∠PEB,
∴∠OB+∠PBE=90°,即∠OBP=90°,
∴OB⊥PB,
∴PB与⊙O相切;
(2)∵$\widehat{AC}$=$\widehat{AD}$,
∴∠ACE=∠ABC,
∵∠CAE=∠BAC,
∴△ACE∽△ABC,
∴$\frac{AC}{AE}$=$\frac{AB}{AC}$,
∴AC2=AE•AB,
∵AC2=2AE2,
∴AE•AB=2AE2,
∴AB=2AE,
∴E为AB的中点.
点评 本题考查了相似三角形的性质和判定,切线的性质,圆周角定理,圆心角、弧、弦之间的关系等知识点,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16.某市政府将对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗,某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价如表:
设购买甲种树苗x棵,承包商获得的利润为y元.请解答下列问题:
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
| 品种 | 购买价(元/棵) |
| 甲 | 20 |
| 乙 | 32 |
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
 如图,∠MON及ON上一点A.
如图,∠MON及ON上一点A.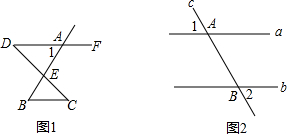
 如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.
如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.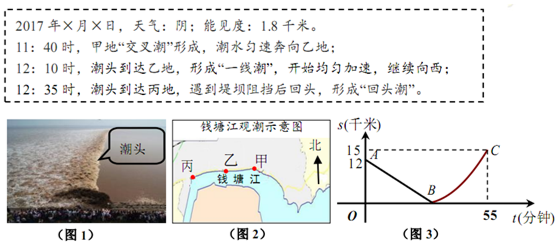

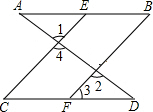
 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°.
如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°.