求当a=1.b=-2时.代数式(a2$-\frac{1}{b}$)(b2$-\frac{1}{a}$)的值．题目和参考答案——青夏教育精英家教网—

题目内容

16．求当a=1，b=-2时，代数式（a²$-\frac{1}{b}$）（b²$-\frac{1}{a}$）的值．

分析直接代入求值即可．

解答解：把a=1，b=-2代入得，
原式=（1$+\frac{1}{2}$）（4-1）=$\frac{9}{2}$．

点评本题主要考查了代数式求值，直接用代入法求解是解答此题的关键．

练习册系列答案

相关题目

6．

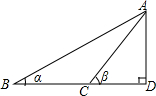如图所示，已知∠ABD=α．△ACD=β，BC=a，则高AD为（　　）

	A．	$\frac{tanα•tanβ}{tanβ-tanα}$•a		B．	（$\frac{1}{tanα}$-$\frac{1}{tanβ}$）•a
	C．	$\frac{1}{tanα-tanβ}$•a		D．	（tanα-tanβ）•a

7．已知，$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=2，则$\frac{a-3c+5e}{b-3d+5f}$=（　　）

4．先化简，后求值：
（1）$\frac{3}{2}$m-（$\frac{5}{2}$m-1）+3（4-m），其中m=-3．
（2）5a²b-[2a²b-2（ab²-2a²b）]-2ab²，其中a=-$\frac{1}{2}$，b=4．
（3）如果代数式（2x²+ax-y+1）-（2bx²-3x+5y-4）的值与字母x所取的值无关，试求代数式$\frac{1}{3}{a^3}-2{b^2}-（{\frac{1}{4}{a^3}-3{b^2}}）$的值．

-a³=a³

a²=|a|²

a³=|a|³

1．

如图，在?ABCD中，E为线段AD上一点，AE=4ED，CE、BD交于点F，若DF=4cm，则BF的长为20cm．

8．赵老师为了响应市政府“绿色出行”的号召，上下班由自驾车方式改为骑自行车方式．已知赵老师家距学校20千米，上下班高峰时段，自驾车的速度是自行车速度的2倍，骑自行车所用时间比自驾车所用时间多$\frac{5}{9}$小时．求自驾车速度和自行车速度各是多少？

5．下面是一个以某种规律排列的数阵：

根据数阵的规律，第n（n是整数）行从左到右数第（n+1）个数是$\sqrt{{n}^{2}+1}$．（用含n的代数式表示）

6．已知$\frac{x}{y}$=$\frac{1}{3}$，那么$\frac{x+y}{x-y}$的值为（　　）

试题分类