题目内容
8.赵老师为了响应市政府“绿色出行”的号召,上下班由自驾车方式改为骑自行车方式.已知赵老师家距学校20千米,上下班高峰时段,自驾车的速度是自行车速度的2倍,骑自行车所用时间比自驾车所用时间多$\frac{5}{9}$小时.求自驾车速度和自行车速度各是多少?分析 设自行车速度为x千米/时,则驾车的速度为2x千米/时,根据题意可得,走20千米,骑自行车所用时间比自驾车所用时间多$\frac{5}{9}$小时,据此列方程求解.
解答 解:设自行车速度为x千米/时,
由题意得,$\frac{20}{x}$-$\frac{20}{2x}$=$\frac{5}{9}$,
解得:x=18,
经检验:x=18是原分式方程的解,且符合题意,
则2x=36.
答:自行车速度为18千米/时,驾车的速度为36千米/时.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
18.如图所示,下列四个选项中,不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列运算中,正确的是( )
| A. | 2x2+3x2=5x2 | B. | x2•x3=x6 | C. | (x2)3=x8 | D. | (x+y)2=x2+y2 |
17.已知点P1(a,2013)和P2(-2012,b)关于原点对称,则(a+b)2015的值为( )
| A. | 1 | B. | -1 | C. | 72015 | D. | -72015 |
18.某超市在“元旦”促销期间规定:超市内所有商品按标价的80%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440×80%=352元,获得的优惠额为:440×(l-80%)+40=128元.
(1)若购买一件标价为800元的商品,则消费金额为640元,获得的优惠额是290元;
(2)若购买一件商品的消费金额a在450≤a<800之间,请用含a的代数式表示优惠额;
(3)某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得150元的优惠额?若能,求出该商品的消费金额.
| 消费金额a(元)的范围 | 100≤a<400 | 400≤a<600 | 600≤a<800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
(1)若购买一件标价为800元的商品,则消费金额为640元,获得的优惠额是290元;
(2)若购买一件商品的消费金额a在450≤a<800之间,请用含a的代数式表示优惠额;
(3)某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得150元的优惠额?若能,求出该商品的消费金额.
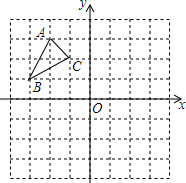 如图,△ABC中A(-2,3),B(-31),C(-1,2).
如图,△ABC中A(-2,3),B(-31),C(-1,2).